Lituus

Courbe étudiée par Cotes et Maclaurin en 1722.
Lituus (mot latin) : bâton des augures romains, ressemblant à la crosse des évêques actuelle. Autre nom : spirale limaçon.

Équation polaire : .
Abscisse curviligne : .
Rayon de courbure : .
Courbe transcendante.

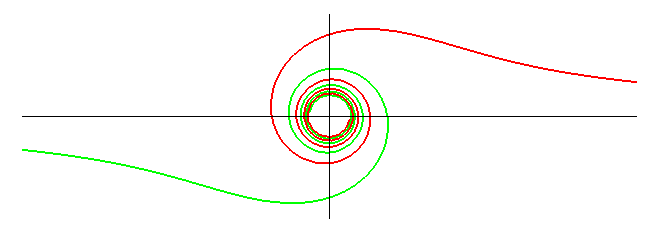Le lituus est le lieu du point M d'un cercle variable centré en O coupant l'axe Ox en A tel que l’aire du secteur circulaire OAM soit constante égale à a²/2.

Le point d'inflexion est obtenu pour q = 0,5 radians, soit près de 30°.

Le lituus est l'inverse de centre O de la spirale de Fermat et la radiale de la clothoïde.

On le retrouve dans les volutes des chapiteaux ioniques :

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres