COURBE DES PONTS SUSPENDUS
Suspension
bridge curve, Hängebrückekurve

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE DES PONTS SUSPENDUS
Suspension
bridge curve, Hängebrückekurve

| Courbe étudiée par François Lavallou en 2008 (Tangente Sup n° 46) |
| Si Paramétrisation cartésienne : Abscisse curviligne : |
La courbe des ponts suspendus est la forme prise par un
fil pesant flexible infiniment mince homogène inextensible suspendu
entre deux points, placé dans un champ de pesanteur uniforme, et
auquel est suspendu par une infinité de fils une ligne pesante horizontale
(le pont).
Notons que dans la réalité d'un pont suspendu,
il n'y a qu'un nombre fini de fils de suspension et que le pont repose
aussi en partie sur les piles extrêmes.
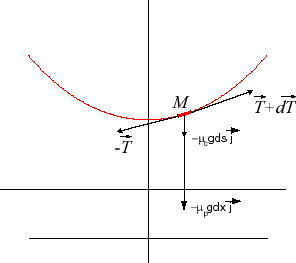
| Avec les notations de la figure ci-contre et celles de
l'encadré ci-dessus ( Ceci se simplifie en |
 |
Si l'on trace une famille de courbes de ponts suspendus
de mêmes longueurs pour des valeurs de k allant de 0 (masse
du pont << masse du cable : chaînette)
à k infini (masse du pont >> masse du cable : parabole)
on obtient les figures ci-contre et ci-dessous montrant le peu de différence
entre les diverses courbes ; la flêche de la parabole est légèrement
plus grande que celle de la chaînette.
 |
 |
Pour un pont suspendu réel, on peut considérer que la masse du cable est négligeable devant celle du pont et que donc le cable prend une forme de parabole.
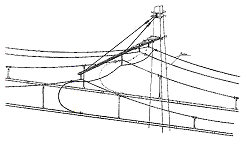
Dans le cas des caténaires ferroviaires, le fil
supérieur et le fil de contact ont des masses du même ordre
donc on pourrait considérer que le raisonnement ci-dessus s'applique,
mais en réalité les fils de suspension sont trop peu nombreux
et le fil supérieur a plutôt une forme de ligne brisée...
 |
 |
 |
Les formules intégrales ci dessus se calculent
pour les différentes valeurs de k :
|
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2018