Pseudo-cycloidale

COURBE PSEUDO-CYCLOÏDALE, PARACYCLOÏDE, HYPERCYCLOÏDE
Pseudocycloidal curve, paracycloid, hypercycloid, Pseudozykloidale Kurve, Parazykloid, Hyperzykloid

Courbes étudiées par Euler en 1750 et 1783, Césaro en 1887.

Les courbes pseudo-cycloïdales sont les courbes vérifiant une équation intrinsèque du type , par analogie avec les courbes cycloïdales, qui vérifient, elles : . Autrement dit, ce sont les courbes, qui, roulant sans glisser sur une droite ont leur centre de courbure décrivant une hyperbole dont un axe est parallèle à la droite (voir à courbe de Mannheim).

Il y a deux cas, suivant le signe de la cte ci-dessus.

Premier cas, cte <0 : PARACYCLOÏDE

Paramétrisation cartésienne : .
Rayon polaire : .
Angle tangentiel cartésien : .
Abscisse curviligne : .
Rayon de courbure : .
Equation intrinsèque 1 : .

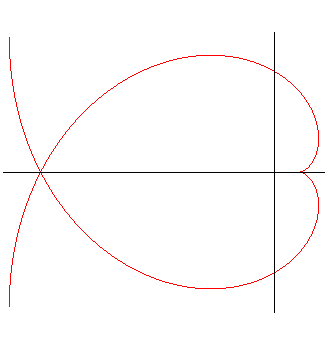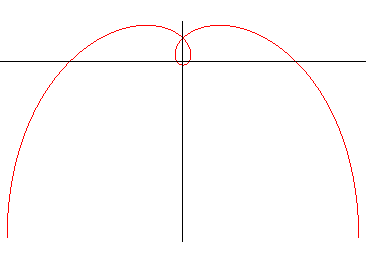
Deuxième cas, cte >0 : HYPERCYCLOÏDE (attention, le terme hypercycloïde est aussi utilisé à la place d'épicycloïde)

Paramétrisation cartésienne : .
Rayon polaire : .
Angle tangentiel cartésien : .
Abscisse curviligne : .
Rayon de courbure :.
Equation intrinsèque 1 : .

REMARQUE : la paracycloïde est l'antipodaire de la spirale du sinus hyperbolique , et l'hypercycloïde est l'antipodaire de la spirale du cosinus hyperbolique . De plus, elles sont développée l'une de l'autre.

Voir les géodésiques du paraboloïde, qui sont des relèvement d'hypercycloïde.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres