Toroïde

TOROÏDE
Toroid, Toroide

Courbe étudiée par Cauchy en 1841, Catalan et Breton des Champs (qui lui a donné son nom) en 1844.
Le nom toroïde vient de tore.

Paramétrisation cartésienne : .
pour l’ellipse : et une distance d à l'ellipse.
Biquartique d'équation cartésienne :
a^8*b^4-2*a^8*b^2*d^2-2*a^8*b^2*y^2+a^8*d^4-2*a^8*d^2*y^2+a^8*y^4-2*a^6*b^6+2*a^6*b^4*d^2-4*a^6*b^4*x^2+6*a^6*b^4*y^2+2*a^6*b^2*d^4+6*a^6*b^2*d^2*x^2+4*a^6*b^2*d^2*y^2+6*a^6*b^2*x^2*y^2-6*a^6*b^2*y^4-
2*a^6*d^6-2*a^6*d^4*x^2+6*a^6*d^4*y^2+4*a^6*d^2*x^2*y^2-6*a^6*d^2*y^4-2*a^6*x^2*y^4+2*a^6*y^6+a^4*b^8+2*a^4*b^6*d^2+6*a^4*b^6*x^2-4*a^4*b^6*y^2-6*a^4*b^4*d^4-8*a^4*b^4*d^2*x^2-8*a^4*b^4*d^2*y^2+6*a^4*b^4*x^4-10*a^4*b^4*x^2*y^2+6*a^4*b^4*y^4+2*a^4*b^2*d^6
+4*a^4*b^2*d^4*x^2-8*a^4*b^2*d^4*y^2-6*a^4*b^2*d^2*x^4-6*a^4*b^2*d^2*x^2*y^2+10*a^4*b^2*d^2*y^4-6*a^4*b^2*x^4*y^2+2*a^4*b^2*x^2*y^4-4*a^4*b^2*y^6+a^4*d^8-2*a^4*d^6*x^2-4*a^4*d^6*y^2+a^4*d^4*x^4+6*a^4*d^4*x^2*y^2+6*a^4*d^4*y^4-2*a^4*d^2*x^4*y^2
-6*a^4*d^2*x^2*y^4-4*a^4*d^2*y^6+a^4*x^4*y^4+2*a^4*x^2*y^6+a^4*y^8-2*a^2*b^8*d^2-2*a^2*b^8*x^2+2*a^2*b^6*d^4+4*a^2*b^6*d^2*x^2+6*a^2*b^6*d^2*y^2-6*a^2*b^6*x^4+6*a^2*b^6*x^2*y^2+2*a^2*b^4*d^6-8*a^2*b^4*d^4*x^2+4*a^2*b^4*d^4*y^2+10*a^2*b^4*d^2*x^4-6*a^2*b^4*d^2*x^2*y^2
-6*a^2*b^4*d^2*y^4-4*a^2*b^4*x^6+2*a^2*b^4*x^4*y^2-6*a^2*b^4*x^2*y^4-2*a^2*b^2*d^8+6*a^2*b^2*d^6*x^2+6*a^2*b^2*d^6*y^2-6*a^2*b^2*d^4*x^4-10*a^2*b^2*d^4*x^2*y^2-6*a^2*b^2*d^4*y^4+2*a^2*b^2*d^2*x^6+2*a^2*b^2*d^2*x^4*y^2+2*a^2*b^2*d^2*x^2*y^4+2*a^2*b^2*d^2*y^6
+2*a^2*b^2*x^6*y^2+4*a^2*b^2*x^4*y^4+2*a^2*b^2*x^2*y^6+b^8*d^4-2*b^8*d^2*x^2+b^8*x^4-2*b^6*d^6+6*b^6*d^4*x^2-2*b^6*d^4*y^2-6*b^6*d^2*x^4+4*b^6*d^2*x^2*y^2+2*b^6*x^6-2*b^6*x^4*y^2+b^4*d^8-4*b^4*d^6*x^2-2*b^4*d^6*y^2+6*b^4*d^4*x^4+6*b^4*d^4*x^2*y^2
+b^4*d^4*y^4-4*b^4*d^2*x^6-6*b^4*d^2*x^4*y^2-2*b^4*d^2*x^2*y^4+b^4*x^8+2*b^4*x^6*y^2+b^4*x^4*y^4=0

Les toroïdes sont les courbes parallèles à l'ellipse, donc les développantes de la développée de l'ellipse.
Le nom provient de ce que les toroïdes ne sont autres que les contours apparents du tore.

La toroïde est le contour apparent du tore

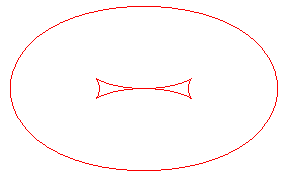
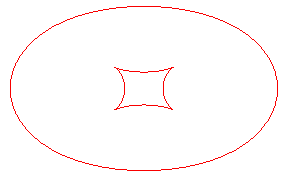
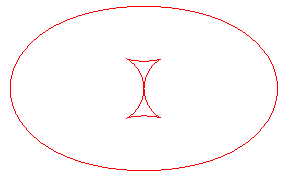
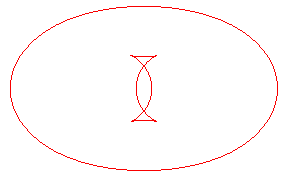
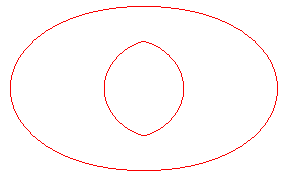
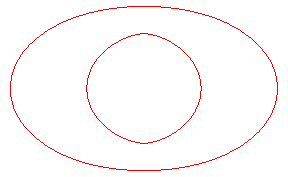
Les toroïdes sont en général formées de deux ovales, sauf lorsqu'on reporte une longueur comprise entre les extremum du rayon de courbure de l'ellipse auquel cas l'une des composantes possède quatre rebroussements situés sur la développée de l’ellipse.
Ci-contre, évolution de la toroïde, quand la distance d à l'ellipse augmente. En vert, la développée de l'ellipse.

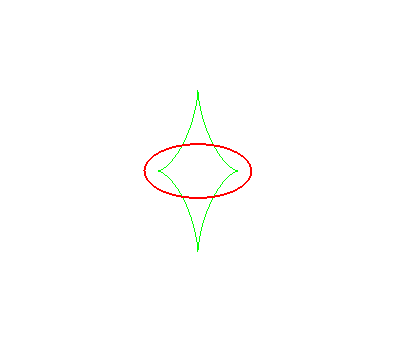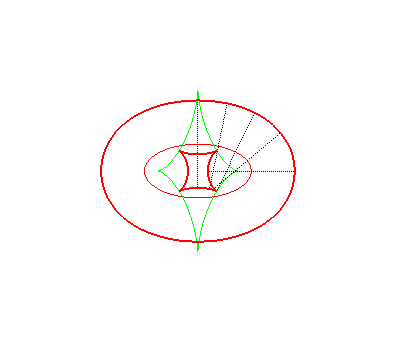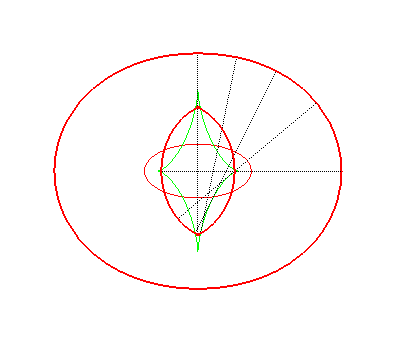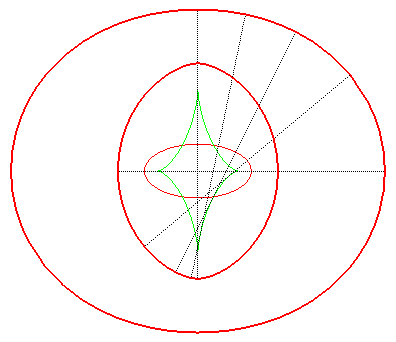Ci-contre, la toroïde (en vert) de l'ellipse bleue, dans le cas d = 2a , longueur qui est aussi le diamètre de l'ellipse.
En prenant la courbe tracée en rouge, on obtient une courbe qui a même diamètre que l'ellipse et qui est de largeur constante, ayant un petit air de triangle de Reulaux, et autre que l'évident cercle circonscrit à l'ellipse.

Voir aussi les glissettes tangentielles de l'ellipse.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

Les toroïdes sont en général formées de deux ovales, sauf lorsqu'on reporte une longueur comprise entre les extremum du rayon de courbure de l'ellipse auquel cas l'une des composantes possède quatre rebroussements situés sur la développée de l’ellipse. Ci-contre, évolution de la toroïde, quand la distance d à l'ellipse augmente. En vert, la développée de l'ellipse.
Ci-contre, la toroïde (en vert) de l'ellipse bleue, dans le cas d = 2a , longueur qui est aussi le diamètre de l'ellipse. En prenant la courbe tracée en rouge, on obtient une courbe qui a même diamètre que l'ellipse et qui est de largeur constante, ayant un petit air de triangle de Reulaux, et autre que l'évident cercle circonscrit à l'ellipse.