Noeud de billard cylindrique

CYLINDRICAL BILLIARD KNOT AND LINK, OR TURK'S HEAD KNOT

Links: Wikipedia
www.mi.sanu.ac.rs/vismath/pennock/index.html
Images made by Alain Esculier.

The cylindrical billiard knot, commonly called "Turk's head knot", is the knot obtained from a closed trajectory of a ball in a cylindrical billiard (we assume that the ball is not subject to gravity!) by modifying the self-intersection points and rather passing alternatively above and below an existing braid.

We talk of a knot of type (q x p) or (p,q) (p and q are coprime) if the ball rebounds p times on each edge and turns q times around the axis (knot experts call them Turk's head knot with p bights, or braids, and q leads, or strands or even coils). Between two rebounds, the curve self-intersects q – 1 times: therefore, there are a total of p (q – 1) crossings.
Parametrization (portions of circular helices): .
NB 1: the English notation for the number q of turns is L, initial of Lead and for the number p of rebounds, it is B,
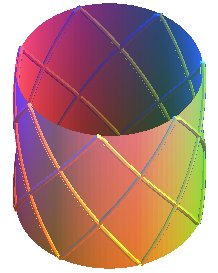
initial of Bight; the knot (p, q) will thus be written: qL x pB.
NB 2: if H is the height of the cylinder and D is its diameter, the total length of the rope is here .

Here, p = 7 and q =3; 7 rebounds on each horizontal edge,
3-1 = 2 crossings on a trajectory between two edges.

The cylindrical billiard knot of type (q x p) can also be obtained with cylindrical sine waves.
Parametrization:

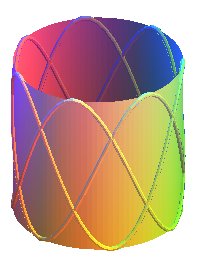With a conical projection on the tangent sphere, we get a spherical sinusoid : .

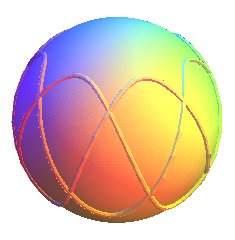With a conical projection on a plane perpendicular to the axis, the cylindrical sine wave is flattened into a polygasteroid with parametrization:;
if the initial version is projected, then the portions of circular helices are projected onto portions of reciprocal spirals:.

With an inversion, the previous curves are transformed into conchoids of roses and portions of Archimedean spirals:
Parametrization:
and

When p > 2q, but only in this case, the curve is topologically equivalent to the crossed polygon or polygram with Schläfli symbol {p/q} (p vertices, with every q-th point connected to one another).

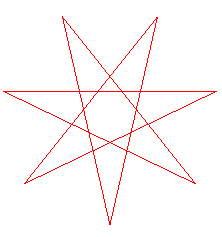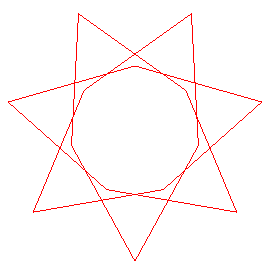On the left, in the case (3x4), passages above or below were alternated.
But if, while going from one edge to the over, we always go above, and if, during the following passage between two edges, we always go below, then we get a toric knot, that differs from the alternated knot as soon as .

Examples (for q = 1, or 2, we refer the reader to toric knots):

p = 2 , q = 3: figure-eight knot

p = 4, q = 3: knot 8.1.18

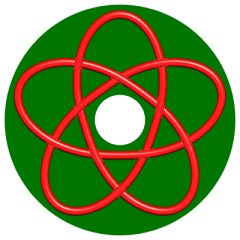
p = 5, q = 3, knot 10.1.123

p = 8, q = 3

Sculpture on wood by J. Mandonnet

p = 3, q = 4: knot 9.1.40

p =5, q = 4: 15 crossings

p =6, q = 5: 24 crossings

p =5, q = 6: 25 crossings

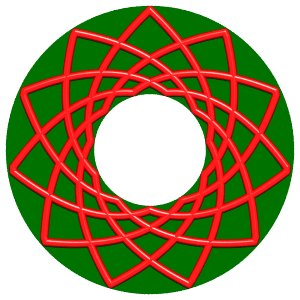
p = 11, q = 5 : 44 crossings

Nota: the case (n, n–1) is equivalent to the alternated generalized trefoil knot with n leaves.

Generalization to links.

Given p and q two non-coprime integers, define d = gcd(p, q), p' = p/d, q' = q/d ; the trajectory of a cylindrical billiard of type (q' x p') and its d – 1 images by the rotations by around the axis of the cylinder, with alternated above/below crossings, form a link with d components, also called Turk's head of type (q x p).
There still are p (q – 1) crossings.
As we will see on the pictures, these links are very popular in Islamic art.

For q = 1 or 2, the link is equivalent to the toric link of the same type.

Moroccan plate, type (2x6) (plus three loops) Handmade Moroccan stucco, type (2x8), Drawings of Eric Broug, specialist of Islamic patterns, type (2x12).

Examples with :

Roman mosaic of the Villa Romana del Casale, in Sicily: type (3x6); Brunnian link.
Entangled in a (2x8). Bottom of a Turkish bottle: type (3x12); Brunnian link too. Painted wood, Damascus: type (4x16) (picture Mohamed Roumi) Logo of the European Society for Mathematics and Art:
type (8x12), non alternated.

Remark: if we authorize any type of crossings, and not only alternating ones, then we get all the possible knots. Indeed, every knot has a projection that is a regular crossed polygon.

See also the polygonal knots, which are equivalent to Turk's heads.
Opposite the type (3x4) knot.

Compare to the rectangular billiard knots.

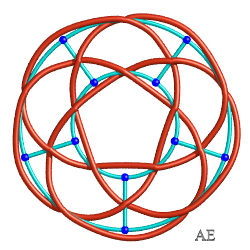
See also the graph associated to the Turk's head of type (q x p) (which has p(q–1) edges), that enables an easy drawing of the knot.
Opposite, the type (3x5) and (4x5) knots, and their graphs with 10 and 15 edges.

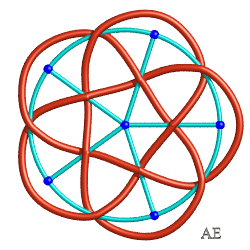Buy Turk's head pendants: www.golden-knots.com/pendant.html

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

We talk of a knot of type (q x p) or (p,q) (p and q are coprime) if the ball rebounds p times on each edge and turns q times around the axis (knot experts call them Turk's head knot with p bights, or braids, and q leads, or strands or even coils). Between two rebounds, the curve self-intersects q – 1 times: therefore, there are a total of p (q – 1) crossings. Parametrization (portions of circular helices): . NB 1: the English notation for the number q of turns is L, initial of Lead and for the number p of rebounds, it is B, initial of Bight; the knot (p, q) will thus be written: qL x pB. NB 2: if H is the height of the cylinder and D is its diameter, the total length of the rope is here .	Here, p = 7 and q =3; 7 rebounds on each horizontal edge, 3-1 = 2 crossings on a trajectory between two edges.
The cylindrical billiard knot of type (q x p) can also be obtained with cylindrical sine waves. Parametrization:
With a conical projection on the tangent sphere, we get a spherical sinusoid : .

With a conical projection on a plane perpendicular to the axis, the cylindrical sine wave is flattened into a polygasteroid with parametrization:; if the initial version is projected, then the portions of circular helices are projected onto portions of reciprocal spirals:.
With an inversion, the previous curves are transformed into conchoids of roses and portions of Archimedean spirals: Parametrization: and
When p > 2q, but only in this case, the curve is topologically equivalent to the crossed polygon or polygram with Schläfli symbol {p/q} (p vertices, with every q-th point connected to one another).


Moroccan plate, type (2x6) (plus three loops)	Handmade Moroccan stucco, type (2x8),	Drawings of Eric Broug, specialist of Islamic patterns, type (2x12).

Roman mosaic of the Villa Romana del Casale, in Sicily: type (3x6); Brunnian link. Entangled in a (2x8).	Bottom of a Turkish bottle: type (3x12); Brunnian link too.	Painted wood, Damascus: type (4x16) (picture Mohamed Roumi)	Logo of the European Society for Mathematics and Art: type (8x12), non alternated.