Notion studied by Roger in 1848. From the Greek brakhisto "the shortest" (therefore written with an "i" and not a "y") and chronos "time". See: Paul Appell: cours de mécanique rationnelle, pages 482 to 485.

 

Differential equation: where  and  is the normal vector of the surface.

A brachistochrone line of a surface is a curve on which a massive point placed in a uniform gravitational field slides without friction in such a way that the travel time is minimal among all the curves joining two points on the curve, whichever those two points may be.
In other words, they are the timewise shortest lines, while the geodesics are the shortest lines in terms of distance.
 

Here is the derivation of the above differential equation:
The conservation of energy gives , hence : the travel time between A and B is therefore ; and thanks to the Lagrange equations, we can prove that the curves minimizing the integral  are solutions of .

Examples (compare to the corresponding geodesics):

    - the brachistochrone lines of a plane that is not horizontal are cycloids with an axis with maximal slope (see brachistochrone for the case of the vertical plane).

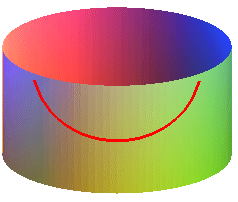
    - the brachistochrone lines of a vertical cylinder are the curves that develop into cycloids with vertical axis.
 

Brachistochrones of cylinders of revolution:

 

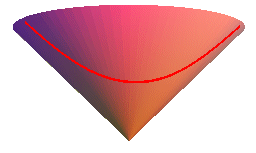
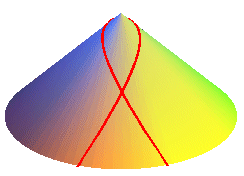
Brachistochrones of cones of revolution:

 

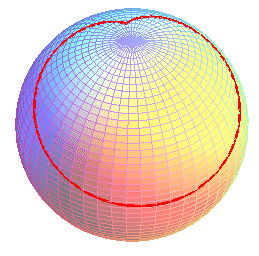
A spherical brachistochrone:

 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2018