ALGEBRAIC CURVE (3D/)

ANAMORPHOSE

ARCHYTAS (CURVE)

ASYMPTOTIC LINE OF A SURFACE

ASYMPTOTIC LINE OF THE TORUS

BALL (SEAM LINE OF THE TENNIS/)

BASIN (3D/)

BERTRAND CURVE

BEZIER CURVE (3D/)

BICYLINDRICAL CURVE

BILLIARD KNOT (CYLINDRICAL/)

BILLIARD KNOT (RECTANGULAR/)

BIQUADRATIC

BITORIC

BORROMEAN RINGS

BRACHISTOCHRONE

BRUNNIAN LINK

CAPAREDA CURVES

CARRICK BEND

CATALAN HELIX

CATENARY ON A SURFACE

CATENARY (CONICAL/)

CATENARY (CYLINDRICAL/)

CATENARY (ELECTRODYNAMIC/)

CATENARY (SPHERICAL/)

CELTIC KNOT

CIRCLE (GEODESIC/)

CIRCLE (CUBIC/)

CIRCLE (SKEW/)

CLELIA

CONIC (SPHERICAL/)

CONTOUR (LINE/)

CREST LINE

CUBIC (3D/)

CURVATURE LINE

CURVATURE (CURVE OF CONSTANT/)

CYCLIC (SPHERICAL/)

CYCLOID (SPHERICAL/)

CYLINDRICAL SINE WAVE

CYLINDRICAL TANGENT WAVE

CYLINDRICAL CURVE

CYLINDRO-CONICAL CURVE

DEFERENT

EDGE OF A DEVELOPABLE RULED SURFACE (CUSPIDAL/)

EIGHT KNOT (FIGURE-/)

ELLIPSE (SPHERICAL/)

ENVELOPE OF A FAMILY OF CURVE WITH ONE PARAMETER

EPICYCLOID (SPHERICAL/)

EVOLUTE

FESTOON OF THE SPINNING TOP

FLOW LINE

GEODESIC

GEODESIC (CIRCLE/)

GEODESIC OF THE TORUS

GRANNY KNOT

GRAPH ASSOCIATED TO A LINK

GYROSCOPE (CURVE OF THE/)

HELIX

HELIX (CATENARY/)

HELIX (CONICAL/)

HELIX (CYLINDRICAL/)

HELIX (ELLIPTIC/)

HELIX (SPHERICAL/)

HELIX OF THE PARABOLOID OF REVOLUTION

HEXAGRAM

HIPPOPEDE OF EUDOXUS

HOROPTER CURVE

HYPOCYCLOID (SPHERICAL/)

INDICATRIX OF CURVATURE OF A 3D CURVE (SPHERICAL/)

INDICATRIX OF TORSION OF A 3D CURVE (SPHERICAL/)

INVOLUTE

ISOHYPSE

JACOB LADDER

KNOT

KNOT (CELTIC LINEAR/)

KNOT (CYLINDRICAL BILLIARD/)

KNOT (FIGURE-EIGHT/)

KNOT (LISSAJOUS/)

KNOT (POLYGONAL/)

KNOT (POLYGRAM/)

KNOT (PRETZEL/)

KNOT (RECTANGULAR BILLIARD/)

KNOT (SQUARE/)

KNOT (TORUS/)

KNOT (TREFOIL/)

LEFT-HANDED 3D CURVE

LIFT OF A PLANAR CURVE ON A SURFACE

LINE TRACED ON A SURFACE

LINE
   ASYMPTOTIC/, CURVATURE/, GEODESIC/, PSEUDOGEODESIC/

LINE (FLOW/)

LINE (MAGNETIC FIELD/)

LINE (TOPOGRAPHIC/):
    CONTOUR/, CREST/, SLOPE/, THALWEG/

LINK

LISSAJOUS CURVE (3D/)

LISSAJOUS KNOT

MAGNETIC FIELD LINE

PANCAKE CURVE

PAPPUS (CONICAL SPIRAL OF/)

PARABOLA (SKEW/)

PARALLEL CURVE

PEEL (CURVE OF THE ORANGE/)

PENDULUM (CURVE OF THE SPHERICAL/)

PENTAGRAM

PIRONDINI (CONICAL SPIRAL OF/)

POLYGRAM (INTERLACED/)

PRECESSION (CURVE OF CONSTANT/)

PRETZEL KNOT

PSEUDOGEODESIC

PURSUIT CURVE

QUARTIC (3D/)

RIDGE LINE

RIGHT-HANDED 3D CURVE

ROSE (CONICAL/)

RHUMB LINE OF A SURFACE

RHUMB LINE OF THE SPHERE

RHUMB LINE OF THE TORUS

RINGS (BORROMEAN/)

SATELLITE CURVE

SEAM LINE OF THE TENNIS BALL

SEIFFERT (SPHERICAL SPIRAL OF/)

SINE WAVE (CYLINDRICAL/)

SINUSOID (SPHERICAL/)

SLANT (CURVE OF EXTREME/)

SLOPE LINE (or LINE OF MAXIMAL SLOPE)

SOLENOID

SOLENOID (TORIC/)

SPHERICAL CURVE

SPHERO-CYLINDRICAL CURVE

SPINNING-TOP (FESTOON OF THE/)

SPIRAL (HYPERBOLIC CONICAL/)

SPIRAL (SPHERICAL/)

SPIRAL OF PAPPUS (CONICAL/)

SPIRAL OF PIRONDINI

SPIRIC

SQUARE KNOT

STEVEDORE KNOT

STRICTION LINE OF A NON DEVELOPABLE RULED SURFACE

TENNIS BALL (SEAM LINE OF THE/)

THALWEG LINE

TOPOGRAPHIC LINE

TORIC CURVE

TORIC CURVE

TORIC KNOT

TORSION (CURVE OF CONSTANT/)

TRACTORY

TREFOIL KNOT

TROCHOID (SPHERICAL/)

TURK'S HEAD

VISIBLE OUTLINE

VIVIANI CURVE

WATER DIVIDE

WINDOW (VIVIANI/)

: curve under consideration.

M: current point on the curve.

direct orthonormal frame, with axes Ox , Oy and Oz.

: Cartesian coordinates of M.

: cylindrical coordinates of M; .

or : spherical coordinates of M ( is the longitude,  is the latitude and  the colatitude).

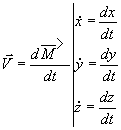, speed vector, V: algebraic speed.

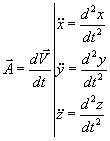, acceleration vector.

(T): tangent, supported by .
(P): osculating plane, supported by  and .

(N): principal normal, orthogonal to (T), in the osculating plane.

(B): binormal, orthogonal to (P), supported by .

s: curvilinear abscissa

(, )

(see also this page for the curvilinear abscissa traced on a surface)

: tangent (unit) vector.

V: absolute speed ().

: normal (unit) vector, supports the principal normal; the plane (M,,) is the osculating plane at M.

: center of curvature at M.

: binormal vector =  (unit) ( = base, or Frenet trihedron).
: radius of curvature, always nonnegative.
is the angle between  and , thus between two infinitely close tangents; j is the angle of curvature; it represents the length of the path on which travels the end of the tangent vector attached to a fixed point.

: radius of torsion of a skew curve.
, defined by  is the angle between two infinitely close osculating planes; the sign convention we used, called Darboux convention, is such that the right-handed curves have a positive torsion; its sign does not depend on the travel sense along the curve;  is the torsion angle; it represents the length of the path on which travels the end of the binormal vector attached to a fixed point.

We have the Frenet formulas:, , .

: curvature ;  ( measures the intensity of the variation of the tangente) .
: torsion ( measures the intensity of the variation of the osculating plane).
Hence the condensed writing of Frenet formulas: .

Cartesian system of equations, parametrization: characterization in terms of x, y and z.

Cylindrical system of equations, parametrization: characterization in terms of ,and z.

Spherical system of equations, parametrization: characterization in terms of r, and.

See the notations for curves traced on a surface on the page dealing with surfaces.
 

bibliography

introduction

2D curves

Back to homepage

surfaces

fractals

polyhedra