PANCAKE CURVE
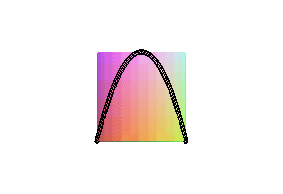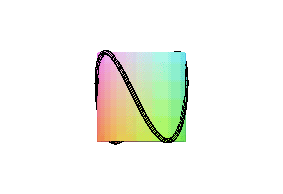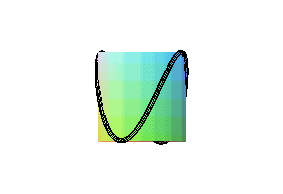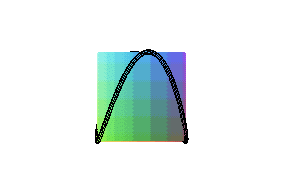
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
PANCAKE CURVE
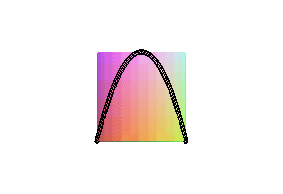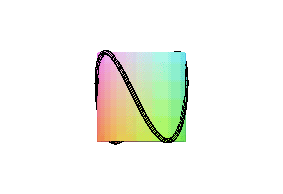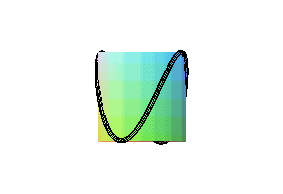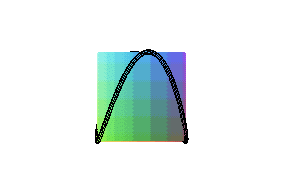
| Since this curve resembles the edge of a curved circular
pancake (when it is being flipped), and it does not have an official name,
I decided to call it "pancake curve".
Opposite, read a text by J.E. Mebius on this topic. |
As far as I know, this curve doesn't have any name of its own. However, it is closely related to a famous item of 19th-century mathematics, the cylindroid surface, discovered by William Kingdon Clifford during his research into the theory of screws. The equation of the cylindroid in 3D Cartesian coordinates commonly reads z = (xx - yy) / (xx + yy). Turning the whole thing thru 90 deg about the Z axis yields z = 2xy / (xx + yy), and there you are: your curve is the intersection of this cylindroid and the unit cylinder about the Z axis. This is generic: cylindroid and cylinder with common axis always intersect in this kind of space curve. |
| Cartesian parametrization:
form #1: Rational biquadratic (3D quartic of the first kind). |
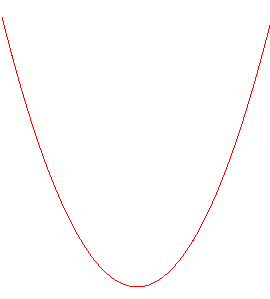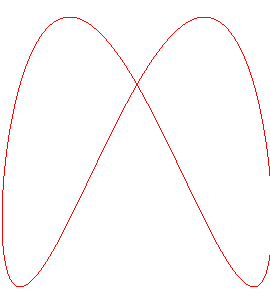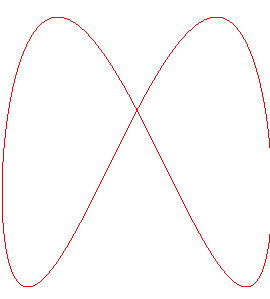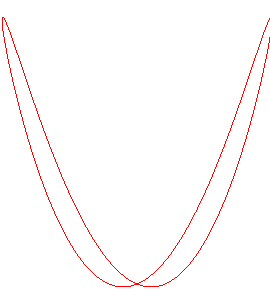
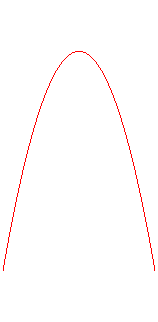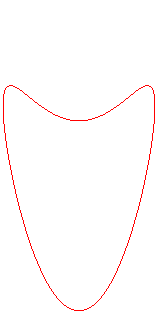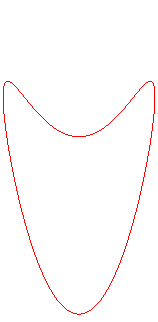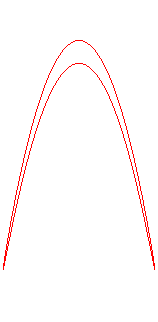
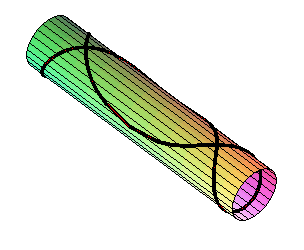
The pancake curve can be obtained as the intersection
between a cylinder of revolution ()
and:
- a hyperbolic
paraboloid with the same axis (
with
for
form #1)
- a Plücker
conoid with the same axis: (
for form #1)
- a parabolic
cylinder with the line at the summit perpendicular to the axis of the
cylinder (
for form #2).
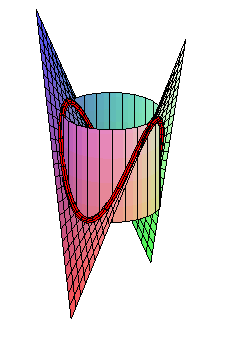
Intersection with a hyperbolic paraboloid |
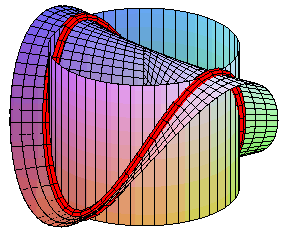
Intersection with a Plücker conoid |
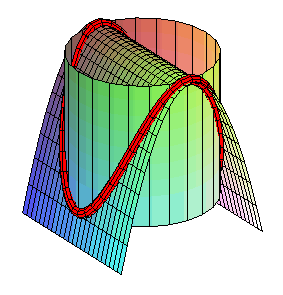
Intersection with a parabolic cylinder |
All in all, there are 6 definitions as intersection between these 4 surfaces.
The pancake curve is a special case of cylindrical sine wave; therefore if we make it roll on a plane, the contact point describes a sinusoid:
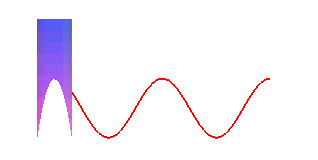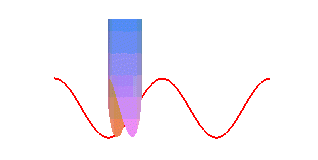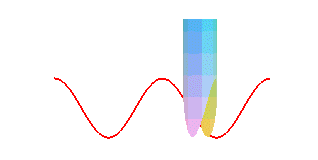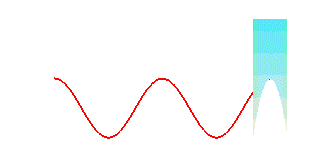
| The projection on xOy is a circle; the projections
on xOz and yOz are isometric lemniscates
of Gerono for form #1 and portions of parabolas
for form #2.
The projections on the planes passing by Oz are
the besaces (first animation).
|
 |
 |
 |
See also at bicylindrical
curve for a similar curve.
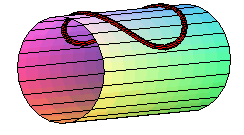
| Despite the name I gave it, the curve must not be mistaken
for another similar one: the curve described by the edge of a circular
pancake with radius b placed on a cylinder with radius a,
parametrized by: |
This curve is transcendental, contrary to the one studied
here.
It develops into a circle when the cylinder is developed: it is a geodesic circle of the cylinder. Moreover, it has double points when |
 |
 |
Compare to the intersection between a hyperbolic paraboloid and a sphere.
See also Hector
Guimard's curve and a sine
torus.
|
The edges of Pringles, which resemble hyperbolic paraboloids, look like the pancake curve... |
|
| The border of this spot seems to be one too. But, being
apparently drawn on a sphere, is it a central projection of a curve of
the flattened pancake onto a sphere?
Parametrization : 8*cos(t)/sqrt(66+2*cos(4*t)), 8*sin(t)/sqrt(66+2*cos(4*t)),
2*cos(2*t)/sqrt(66+2*cos(4*t)) : |
 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2021