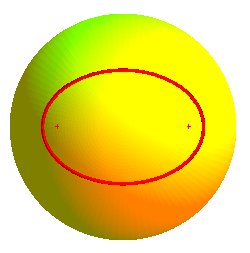
Spherical ellipse
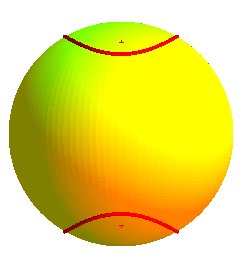
Spherical hyperbola
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
SPHERICAL ELLIPSE, HYPERBOLA

Spherical ellipse |

Spherical hyperbola |
| Curve studied by Fuss in 1788, Steiner in 1827, Chasles
in 1831.
Other name: spherical conic. Website: www.geometrie.tuwien.ac.at/theses/pdf/diplomarbeit_tranacher.pdf |
|
Spherical coordinates of the foci F, F': Bifocal equation of the spherical ellipse on the sphere with radius R: Bifocal equation of the spherical hyperbola: Cartesian equation of the whole curve: section of the sphere
Cartesian parametrization: |
The spherical ellipse is the locus of the points on a
sphere for which the sum of the distances (taken on the sphere) to two
fixed points F and F' on the sphere is a constant. In other
words, it is the result of the classic gardener's method for the planar
ellipse,
transposed for the sphere.
With the above notations, the locus of the points satisfying
is composed of the previous ellipse and its symmetric image with respect
to xOy; the reunion of the two ellipses can therefore be referred
to as "spherical hyperbola".
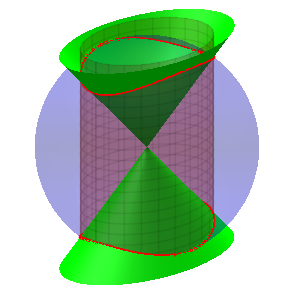
Using the formulas of spherical
trigonometry, one can prove that the spherical hyperbola is the intersection
between the sphere and an elliptic cylinder passing through the center
of the sphere. It is therefore a lift
of an ellipse on a sphere.
It is also an algebraic curve of degree 4, intersection
of all the quadrics of the beam generated by the sphere and the cylinder
(remarkable examples are represented above).
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2018