HELIX or CURVE OF CONSTANT SLOPE
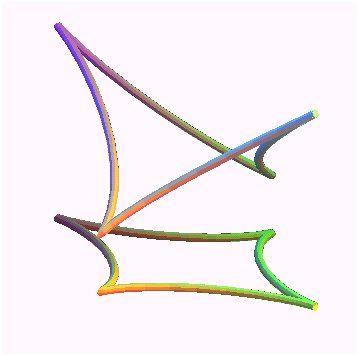
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
HELIX or CURVE OF CONSTANT SLOPE
| From the Latin "helix", derived itself from the Greek
"eliks": spiral.
Other names: curve of equal slope, slope line, isocline curve. |
| The fixed plane being xOy, differential condition: |  |
| i.e. in Cartesian coordinates: |  |
|
Cartesian parametrization knowing the base of the helix, parametrized by  : |
 |
Radii of curvature and torsion, 
being the radius of curvature of the base: |
 et  |
Differential equation of the helices traced on the surface  ,
using the Monge notations: |
coming |
|
Cylindrical equation of the helices traced on the surface of revolution  : |
 |
The helices are the curves the tangents of which form
a constant angle a with respect to a fixed plane
(P0), or a fixed direction d
(orthogonal to (P0)).
Therefore, the notion of helix in mathematics is more
connected to a mountain road with constant slope than to the helix of a
boat!
Concretely, we get a mathematical helix by cutting a
right triangle 
out of a cardboard, placing it vertically on a plane and deforming it:
the hypothenuse takes the shape of a helix.
Necessary conditions for a curve to be a helix:
- curve for which the spherical
indicatrix of curvature is planar (therefore included in a circle).
- curve the principal normals of which remain parallel
to a fixed plane (equal to (P0)).
- curve the binormals of which form a constant
angle with respect to a fixed direction (the same as the tangents).
- curve for which the spherical
indicatrix of torsion is planar (therefore included in a circle).
- curve the torsion of which is proportional to
the curvature (Lancret theorem).
- trajectory of a movement for which the second,
third and fourth derivative vectors are coplanar.
- geodesic
of a cylinder (the cylinder generated by the lines parallel to
d)
- in other words, if we develop the cylinder on which the helix is traced,
the helix becomes a straight line.
A helix is entirely defined by its projection on (P0) (its base) and the angle a.
Examples (note that the helices are described by their
base or the surface on which they are traced):
- the straight line (lines on a surface
are therefore helices of this surface)
- the cylindrical
helix (base = circle)
- the conical
helix (traced on a vertical cone of revolution, base = logarithmic
spiral)
- the elliptic
helix (base = ellipse)
- the spherical
helix (traced on a sphere, base = epicycloid)
- the helix
of the paraboloid (base = involute of a circle).
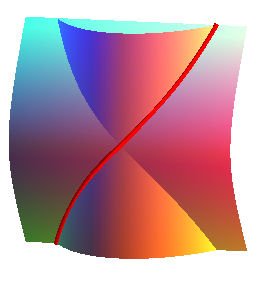
- the helix
of the one-sheeted hyperboloid (traced on the one-sheeted hyperboloid)
- the striction
line of the milk carton
- the catenary helix (base = catenary):  ( );
it is traced on the hyperbolic cylinder  ,
as well as the surface  ,
which is a surface of revolution when a = b.
Curve studied by Catalan in 1878. The catenary helix is the generatrix of the minimal helicoid. |
 |
- the torus helix (traced on
the torus, the reference
plane being orthogonal to the axis of the torus):
 |
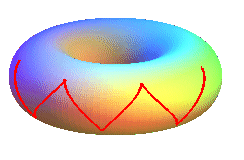
Torus helix with slope 1 |
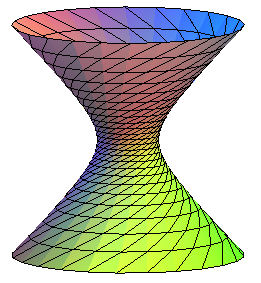
| Example of determination of the helices on a surface:
those of the hyperboloid
of revolution: x² + y² = z² +1, parametrized by
x = cosh u cos v, y = cosh u sin v, z = sinh u. Write dz/ds = tan a, i.e. dx² +dy² = dz²
cot² a, hence, here:
i.e. sqrt(cot²a - tanh² u) du = dv, from which we get v as a function of u. For a = pi/4 we get the included lines. The helices with cot a = 2 were traced opposite.
|
 |
See also the surfaces
of equal slope.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018