The curve  of the plane xOy can be lifted on the surface  as the curve . The curve  can be lifted on the surface of revolution  as the curve .

The lift of a plane curve on a surface is the intersection between the cylinder built on the curve perpendicularly to its plane and the surface. Therefore, it is the maximal curve traced on the surface for which the orthogonal projection is the plane curve.

Examples:
    - the lifts of straight lines on a surface are the plane curves traced on the surface.
    - the lifts of circles are the cylindrical curves.
    - the clelias are lifts of roses on a sphere, whereas the basins are lifts of them on hyperbolic paraboloids, and conical roses, lifts on cones of revolution.
    - the spherical ellipse is a lift of ellipse on a sphere.
    - the conical helix is a lift of a logarithmic spiral, whereas the conical spiral of Pappus is a lift of the Archimedean spiral.
    - the spherical helices are lifts of epicycloids.
    - the helices of the hyperbolic paraboloid (placed vertically) are lifts of involutes of circles.
    - the geodesics of the paraboloid of revolution are lifts of hypercycloids.
 

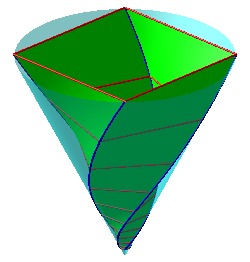
Conical lifts of Archimedean spirals on the left, logarithmic spirals on the right.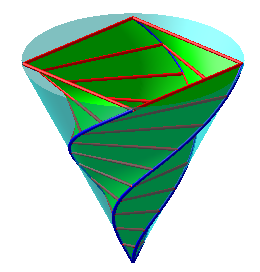
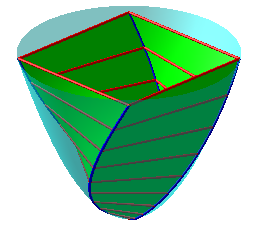
Lifts on a hyperbolic paraboloid of Archimedean spirals on the left, logarithmic spirals on the right.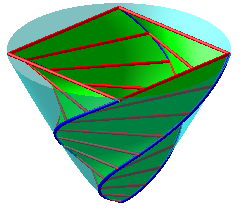

 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2018