COURBE DE BÉZIER 3D
Lien vers une
figure manipulable à la souris
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE DE BÉZIER 3D
Lien vers une
figure manipulable à la souris
| Courbe étudiée par Bézier en 1954
et par de Casteljau.
Pierre Bézier (1910 - 1999) : ingénieur à la régie Renault. |
Paramétrisation affine : 
(soit  )
où les 
sont les polynômes de Bernstein :  .
Courbe algébrique polynomiale de degré £ n. |
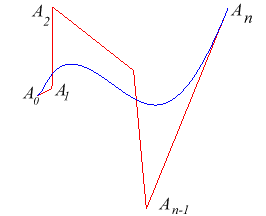
Une ligne brisée 
étant donnés (appelée polygone de contrôle,
les Ak étant les points
de contôle), la courbe de Bézier associée est la courbe
de paramétrisation ci-dessus ; la courbe passe par A0
(pour t = 0) et An (pour
t
= 1), et la portion qui joint ces points est tracée dans l'enveloppe
convexe des points de contrôle ; la tangente en A0
est
(A0A1)
et celle en An (An-1An).
Construction récursive (algorithme de de Casteljau):
Le point 
est le barycentre de 
et 
où 
sont les points courants respectifs des courbes de Bézier de points
de contrôle 
et 
; de
plus la droite 
est la tangente en
à la courbe de Bézier.
Réciproquement, toute courbe algébrique 3D polynomiale est une courbe de Bézier avec unicité du polygone de contrôle associé, une fois les extrêmités de ce polygone choisies arbitrairement sur la courbe.
Les courbes de Bézier 3D sont des cas particuliers de courbes splines 3D.
Leurs projections coniques planes sont les courbes
de Bézier rationnelles planes.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2000