Notion étudiée par Hermann Brunn en 1892, et par John Milnor en 1954. Autre nom : chaîne borroméenne. Sites :  fr.wikipedia.org/wiki/Entrelacs_brunnien katlas.org/wiki/Brunnian_link www.maths.ed.ac.uk/~aar/papers/liangmislow.pdf www.knotplot.com www.aesculier.fr Images réalisées avec povray par Alain Esculier.

Un entrelac est dit brunnien s'il est formé d'un certain nombre de boucles (chacune non nouée), dont aucune n'est libre, mais qui sont libérées dès qu'on enlève l'une quelconque d'entre elles.

Il a été démontré en 1987 qu'aucun entrelac brunnien à 3 boucles ou plus ne peut être formé uniquement de cercles (voir Aigner, Ziegler, Proofs from the book 5. edition p. 95 à 102) .

Exemples :
    - tout entrelac non trivial à deux boucles est brunnien.
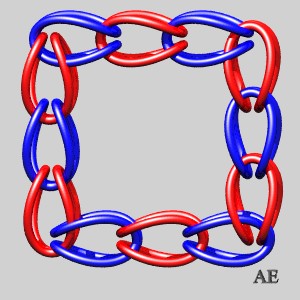
    - la chaîne fermée formée de doubles boucles en U de l'image d'en-tête montre qu'il existe un entrelac brunnien à nombre quelconque de boucles.
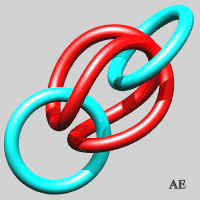
    - on peut former une version non fermée de la chaîne précédente, à condition de mettre deux anneaux bloqueurs aux extrémités ; la première étape n'est autre que l'entrelac borroméen :

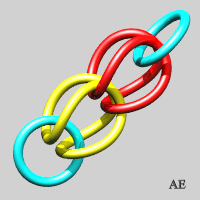
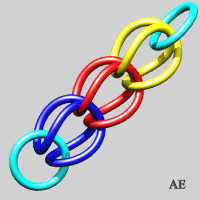
    - On peut aplatir ces anneaux (voir sur le site d'Alain Esculier une animation montrant l'équivalence entre les deux séries) :

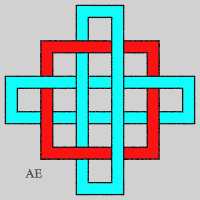
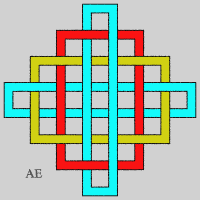
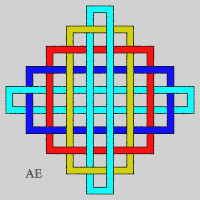
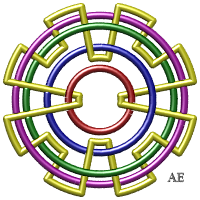
    - On obtient une autre suite d'entrelacs brunniens à n composantes en plaçant n – 1 cercles concentriques et en les enlaçant avec une n-ième composante de sorte que l'ensemble soit enlacé, mais brunnien.
La figure possède  croisements (nombre supérieur à partir de n = 5 au 8n de la figure d'en-tête), mais ce n'est pas le nombre minimal de croisements. Le cas n = 3 redonne aussi l'entrelacs borroméen.

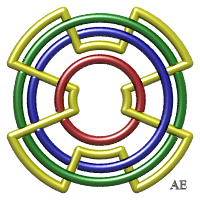
    - pour fabriquer un entrelac brunnien à 3 boucles, poser deux boucles l'une sur l'autre et passer la troisième au dessus de celle du dessus et en dessous de celle du dessous ; ce faisant, on n'obtient pas un unique type d'entrelacs : par exemple, une famille infinie d'entrelacs de ce type est formée des bonnets turcs de type (3n, 3) (donc aussi des polygrammes entrelacés de type {3n/3}), possédant 6n croisements.
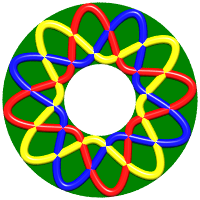
On remarquera dans les exemples ci-dessous que la boucle rouge est sur la bleue qui est sur la jaune qui est sur la rouge...

Type (3,3) : c'est l'entrelac borroméen.	Type (6,3) : 12 croisements voir un exemple sculpté en bas de page.	Type (9,3) : 18 croisements	Type (12,3) : 24 croisements

Malheureusement, les bonnets turcs de type (pn, p), avec un nombre de composantes p > 3 et alternance dessus-dessous, sont non brunniens (donc aussi les polygrammes entrelacés de type {pn/p}). Quand p est impair, les composantes sont tout de même deux à deux non nouées.
 

Ci-contre, les cas (5,5), (7,7) et (15,5) : si les composantes sont 1, 2,.., n en tournant vers la droite, et , x est sous y si y – x est impair, et sur y si y – x est pair. Tout groupe de 3 composantes consécutives forme donc un entrelac borroméen, et est donc noué. Par contre, certains trios comme 1,2,4 sont triviaux. Voir une version polygonale sur cette page.

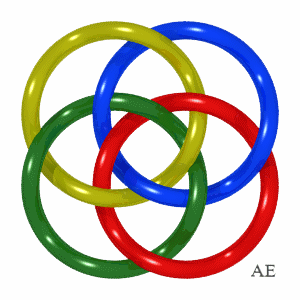
Quand p est pair, la situation est "pire" puisque toutes les composantes sont liées entre elles (figure de gauche). Dans le cas (4,4), on peut améliorer les choses en modifiant les croisements : dans la figure de droite, en tournant à droite, chaque composante est sous la suivante, vert est sous bleu, et rouge est sous jaune. Et parmi les 4 trios, l'un est trivial (rouge bleu jaune) et les 3 autres sont borroméens donc noués.

 

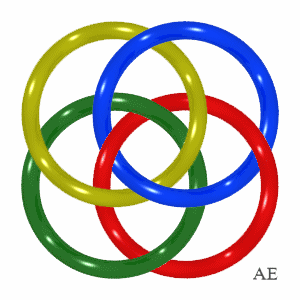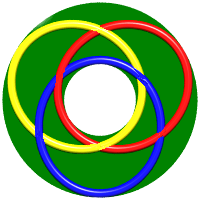
Mais voici un exemple d'entrelac brunnien à 4 boucles découvert par Brunn lui-même en 1892. Notons que contrairement aux apparences, les anneaux ne sont pas plans. Bien vérifier que tout groupe de 3 anneaux est formé de 3 anneaux libres, mais que chaque anneau est prisonnier des 3 autres.

On présente dans la suite quelques exemples "quasi"-brunniens, mais cependant non brunniens.
 

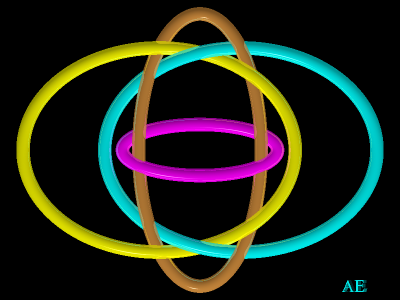
5 boucles, 1, 2, 3, 4, 5 ; en tournant vers la gauche : 1 est sous 2, 2 sous 3, 3 sous 4, 4 sous 5, 5 sous 1 ; de plus, 1 est sous 3 et sur 4,  et 2 est sous 4 et sur 5, 3 est sous 5. Toutes les paires sont non nouées, le trio 1-2-3 est non noué, mais le trio 1-2-5 l'est...
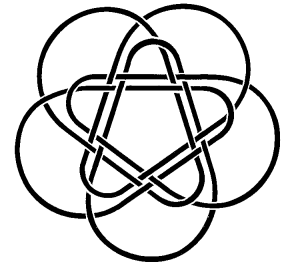Même phénomène pour cet entrelac à 5 boucles dénommé croix de Borromée. En partant du haut, on note les boucles 1,2,3,4, et on note 5 la boucle centrale. 1 et 3 sont sous 2 et 4, 5 est sous 1 et 3, et sur 2 et 4. Toutes les paires sont non nouées, les 4 trios externes et les 2 trios en croix sont triviaux, mais 4 trios comportant la boucle centrale sont des entrelacs borroméens, donc noués. Tous les quatuors sont noués.
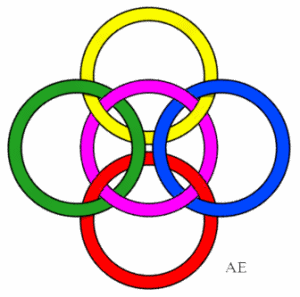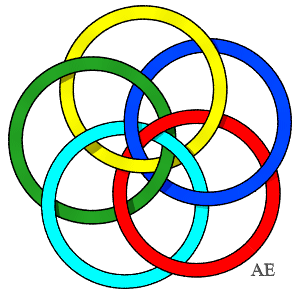
Autre entrelacs à 5 boucles. Toutes les paires sont non nouées, les 5 trios d'anneaux consécutifs sont triviaux, mais les 5 autres sont borroméens. L'entrelac est donc non équivalent au précédent.
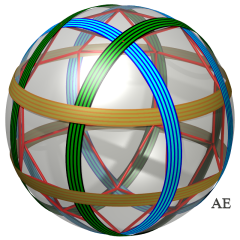
Cet entrelac à 6 boucles est associé au rhombicuboctaèdre. Il est obtenu par dédoublement des trois boucles borroméennes associées à l'octaèdre. Chacun des 8 trios tricolores de cercles forme un trio d'anneaux de Borromée, et est donc noué. Cependant, si l'on coupe deux boucles de même couleur, l'ensemble se dénoue.

 

De gauche à droite :  - décoration église grecque à Vienne ; c'est un bonnet turc alterné de type (6, 3) qui est bien brunnien.  -stèles funéraires en Turquie. La première vient de la forteresse de Bodrum : même type que le précédent. La deuxième vient du musée archéologique de Milas. Non alterné, les boucles sont deux à deux nouées.

Photo : Stacey Demartini

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2022