COURBE DE LA CRÊPE
Pancake
curve, Pfannkuchenkurve
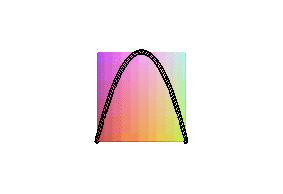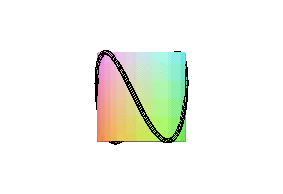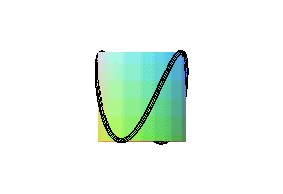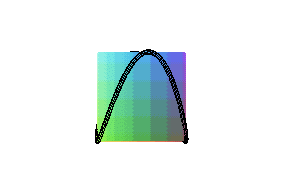
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE DE LA CRÊPE
Pancake
curve, Pfannkuchenkurve
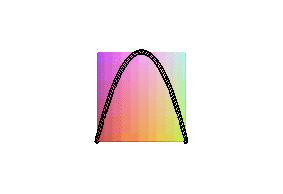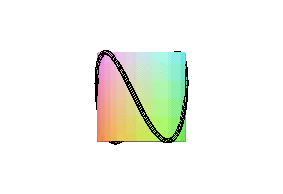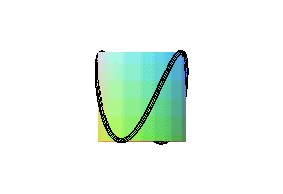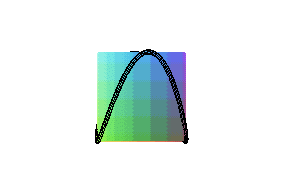
| Cette courbe ressemblant au bord d'une crêpe circulaire
courbée (ce qui arrive lorsqu'on la fait sauter), nous avons donné
le nom de "courbe de la crêpe" à cette courbe qui n'en possède
pas d'officiel.
Lire ci-contre un texte de J.E. Mebius à ce sujet. |
As far as I know, this curve doesn't have any name of its own. However, it is closely related to a famous item of 19th-century mathematics, the cylindroid surface, discovered by William Kingdon Clifford during his research into the theory of screws. The equation of the cylindroid in 3D Cartesian coordinates commonly reads z = (xx - yy) / (xx + yy). Turning the whole thing thru 90 deg about the Z axis yields z = 2xy / (xx + yy), and there you are: your curve is the intersection of this cylindroid and the unit cylinder about the Z axis. This is generic: cylindroid and cylinder with common axis always intersect in this kind of space curve. |
| Paramétrisation cartésienne :
forme 1 Biquadratique (quartique 3D de première espèce) rationnelle. |
On obtient la courbe de la crêpe comme intersection
d'un cylindre de révolution ()
avec :
- un paraboloïde
hyperbolique de même axe (
avec
pour
la forme 1)
- un conoïde
de Plücker de même axe : (
pour la forme 1)
- un cylindre
parabolique de droite sommitale perpendiculaire à l'axe du cylindre
( pour la forme
2).
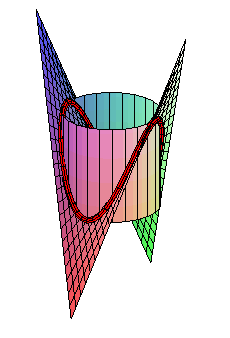
Intersection avec un PH |

Intersection avec un conoïde de Plücker |
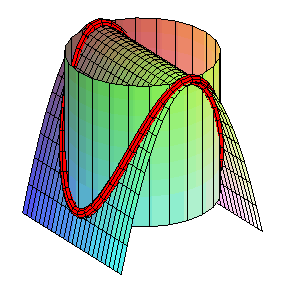
Intersection avec un cylindre parabolique |
En tout il y a donc 6 définitions comme intersections de ces 4 surfaces.
La courbe de la crêpe est un cas particulier de couronne sinusoïdale ; si donc on la fait rouler sur un plan, le point de contact décrit une sinusoïde :
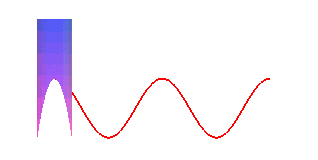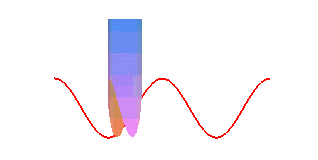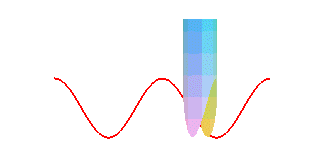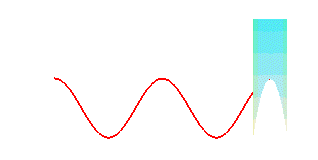
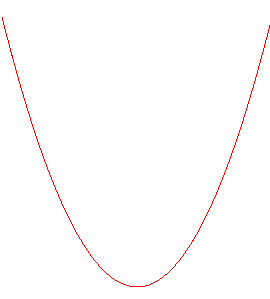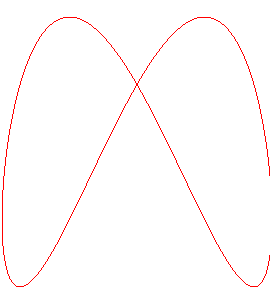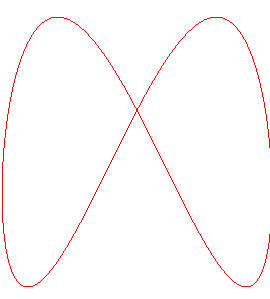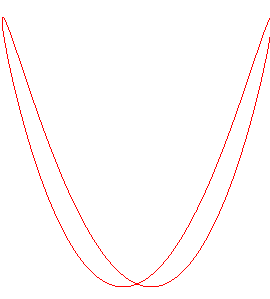
| La projection sur xOy est un cercle ; les projections
sur xOz et yOz sont deux
lemniscates
de Gerono isométriques pour la forme 1 et deux portions de parabole
pour la forme 2.
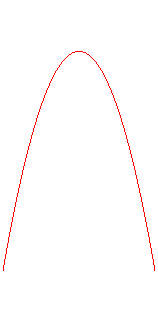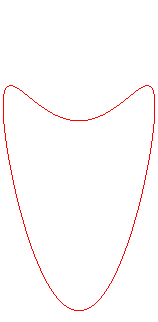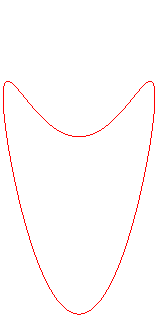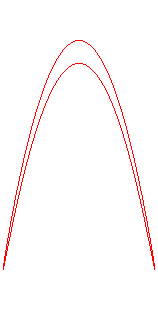
Les projections sur les plans passant par Oz sont
les besaces (première
animation).
|
 |
 |
 |
Voir aussi à bicylindrique
pour une courbe ressemblante.
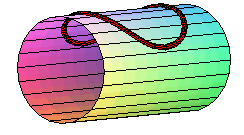
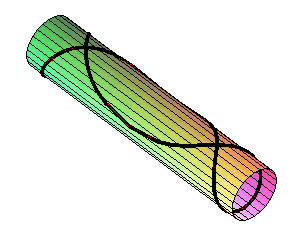
| Malgré le nom que nous avons donné à
cette courbe, il ne faut pas la confondre avec une deuxième courbe
ressemblante, la courbe figurant le bord d'une crêpe circulaire de
rayon b posée sur un cylindre de rayon a, ayant pour
paramétrisation : |
Cette courbe est transcendante, contrairement à
celle qui nous occupe ici.
Elle se développe en un cercle quand on développe le cylindre : c'est un cercle géodésique de ce cylindre. De plus, elle possède des points doubles dès que |
 |
 |
Comparer avec l'intersection d'un paraboloïde hyperbolique avec une sphère.
Voir aussi la surface
d'Hector Guimard et un tore
sinusoïdal.
|
Les pringles, en forme de paraboloïdes hyperboliques, ont un bord en courbe de la crêpe aplatie. |
|
| La bordure de ce spot semble en être une aussi.
Mais, étant apparemment tracée sur une sphère, est-ce
une projection centrale d'une courbe de la crêpe aplatie sur une
sphère ?
Paramétrisation : 8*cos(t)/sqrt(66+2*cos(4*t)), 8*sin(t)/sqrt(66+2*cos(4*t)),
2*cos(2*t)/sqrt(66+2*cos(4*t)) : |
 |
| Aussi le bord des capelines ! |
 |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2020