| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
ENTRELACS
Link
(or interlacing), Verschlingung
| Autre appellation : nœuds emboités.
Référence : Dale Rolfsen, Knots and Links (1976). |
Un entrelacs est un ensemble fini de nœuds
enlacés. Plus précisément, c'est une classe d'équivalence
d'ensembles finis de courbes de
fermées sans point double et sans points communs, deux ensembles
de courbes étant équivalents si on peut déformer dans
chaque courbe de l'un en une courbe de l'autre, de façon continue,
chaque courbe restant constamment fermée sans point double et sans
point commun avec une autre tout au long de la transformation.
Le nombre de croisements d'un entrelacs est le nombre minimum de points doubles des projections planes (sans point d'ordre supérieur ou égal à 3) de ses représentants. Un entrelacs dont un représentant a une projection sans croisement est dit trivial.
Un brin étant choisi dans chacun de deux entrelacs, la somme correspondante des deux entrelacs est l'entrelacs obtenu en coupant le brin choisi de chacun des deux entrelacs et en recollant les bouts. On définit alors un entrelacs premier comme ne pouvant être somme de deux entrelacs non triviaux.
Voici la table de Rolfsen des premiers entrelacs premiers,
à deux brins ou plus (le symbole
donnant le nombre de croisements N, le nombre de brins n,
et le numéro d'ordre p parmi les entrelacs à N
croisements) :
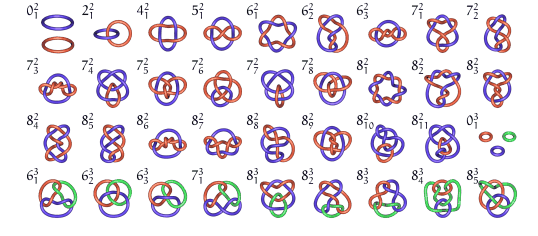
Les six premiers sont des entrelacs
de bretzel.
Voir aussi le graphe
permettant de coder chaque entrelacs.
Table plus complète dans l'atlas
des noeuds.
Exemples, avec la notation N.n.p (N = nombre de croisements, n = nombre de brins, p = numéro d'ordre donné par Rolfsen) :
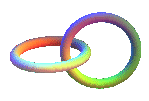  Le plus simple des entrelacs : celui de Hopf 2.2.1 qui est aussi l'entrelacs torique de type (2,2) ; la somme de n entrelacs de Hopf donnant un entrelacs à n + 1 anneaux comme ceux des Jeux. |
  |

Entrelacs de Whitehead 5.2.1 |
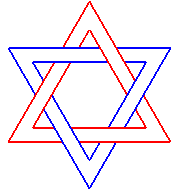  |

Anneaux de Borromée 6.3.2 |
  |
Voir aussi le noeud
de Carrick, les entrelacs brunniens,
qui deviennent triviaux lorsque l'on supprime l'une des composantes, les
entrelacs
de billard, les bonnets
turcs, les entrelacs de bretzel,
les entrelacs celtiques linéaires,
l'entrelacs de l'icosidodécaèdre,
les surfaces de Seifert,
qui remplissent un entrelacs, le collier
d'Antoine, qui est limite d'une suite d'entrelacs.
 |
On pourra remarquer que le tissage représenté à gauche est en fait un entrelacs trivial. C'est d'ailleurs la raison pour laquelle il est réalisable en papier crépon sans déchirure ! |  |
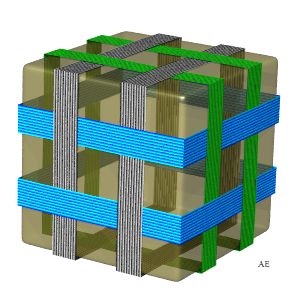 |
Ce cerclage de cube forme un entrelacs de 6 boucles à
24 croisements qui est lié au rhombicuboctaèdre.
A droite, deux versions planes du même entrelacs ; remarquons la symétrie d'ordre 4 pour l'un, et d'ordre 3 pour l'autre. |
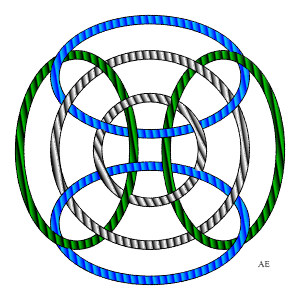 |
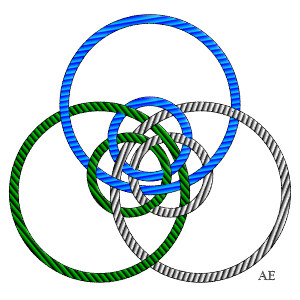 |
Liens :
Liste des entrelacs premiers : katlas.org/wiki/The_Thistlethwaite_Link_Table
Applette java permettant de retrouver le code
de Gauss d'un entrelacs à partir de son tracé : knotilus.math.uwo.ca/javasketch.php
Site permettant de retrouver un entrelacs premier à partir de
son code de Gauss
: knotilus.math.uwo.ca
Site de Christian Mercat, pour apprendre à créer soi-même
des entrelacs : www.entrelacs.net/
Logiciel de Géraud Bousquet
pour dessiner des entrelacs à partir d'un graphe
www.math.utk.edu/~morwen/index.html
www.clanbadge.com/knots.htm
Vitrail
de l'abbaye d'Aubazine
mathouriste.canalblog.com
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2022