Courbe étudiée par Blaschke en 1908 [Mh. Math. Phys. 19, p. 194] Voir aussi [Loria 3d] p. 160.

 

Paramétrisation cartésienne :  tracée sur l'hyperboloïde , avec . Pour  , , on retrouve la droite x = a, by = az. Équation polaire de la projection sur xOy : .

Nous considérons ici l'hélice de l'hyperboloïde de révolution à une nappe d'axe vertical, courbe de pente constante  par rapport à un plan horizontal.
 

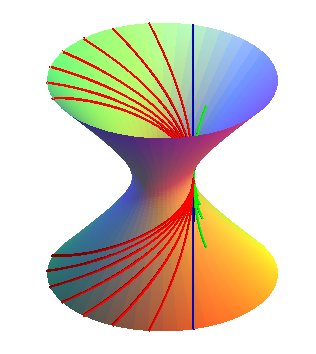
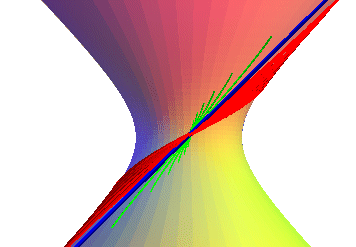
Vue des 3 types d'hélices ;    - en rouge pour une pente < b/a, l'hélice va à l'infini   - en bleu, la droite de pente b/a.   - en vert pour une pente  > b/a ; la courbe est limitée  (sa projection sur xOy ne peut dépasser le cercle de rayon ).

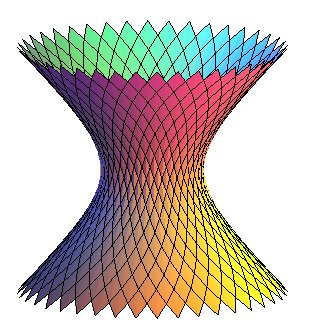
Attention, si l'hélice circulaire est bien l'intersection d'un hélicoïde droit avec un cylindre, cette méthode ne donne pas l'hélice du H1, mais la courbe suivante, non dénommée :

Intersection de l'hélicoïde  avec l'hyperboloïde . Paramétrisation cartésienne : 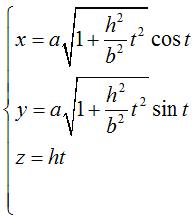 ; la figure ci-contre a été tracée à l'aide de la paramétrisation  dont les lignes de coordonnées sont les courbes qui nous occupent.
Relèvement sur l'hyperboloïde de la spirale , asymptote à la spirale d'Archimède .

 

Visualisation de la construction de ces courbes (par Robert March).

...réalisée par Alain Esculier.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2018