LIGNE D'ÉCOULEMENT D'UNE SURFACE
Flow
line of a surface

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
LIGNE D'ÉCOULEMENT D'UNE SURFACE
Flow
line of a surface




| Courbes étudiées par C. Piquet en 2002. |
| Équation différentielle (issue de
la relation fondamentale de la dynamique) : Ce système différentiel s'écrit,
pour une surface d'équation
z = f(x, y) : |
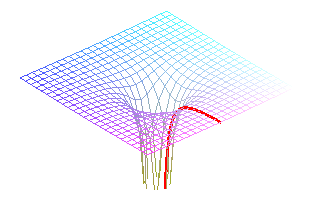
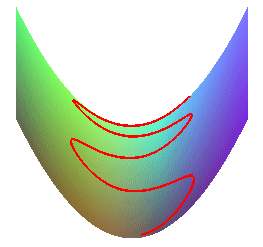
Les lignes d'écoulement d'une surface sont les trajectoires de points matériels liés à la surface soumis à un champ de pesanteur vertical (on les réalise physiquement en faisant rouler une bille polie sur la surface).
Lorsque la vitesse est nulle la ligne d'écoulement est tangente à la ligne de pente passant par le point, mais ce n'est en général plus le cas sinon.
On remarque que l'intensité de la pesanteur g > 0, n'influe pas sur la forme des courbes (même si elle influe sur la vitesse à laquelle elles sont parcourues). Si, par contre, on fait g = 0 dans les équations ci-dessus, on trouve d'autres courbes, qui ne sont autres que les géodésiques de la surface.
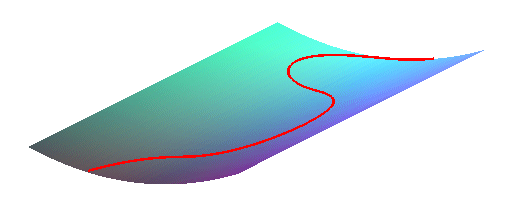
| les lignes d'écoulement d'un plan incliné sont des paraboles ou des droites : |
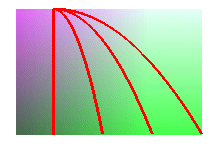 |
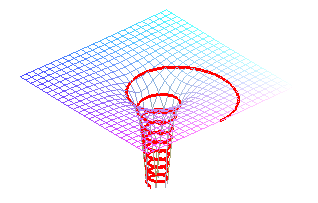
| les lignes d'écoulement d'un cylindre circulaire vertical sont des courbes se développant en des paraboles ou des droites |
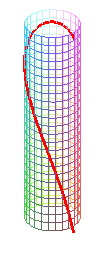 |
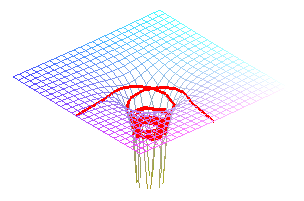
| Les lignes d'écoulement d'une sphère ne sont autres que les courbes du pendule sphérique. | 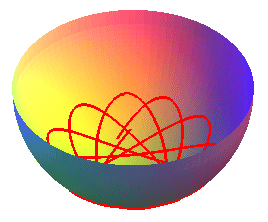 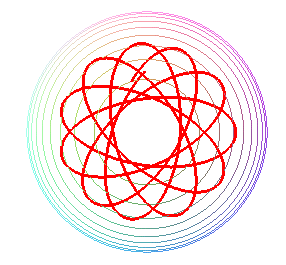 |
Une goutte de pluie tombe dans la gouttière.... |
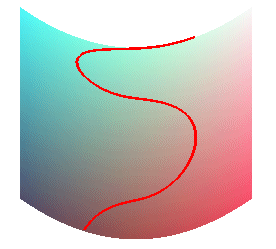 
|
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
, Jacques MANDONNET 2002