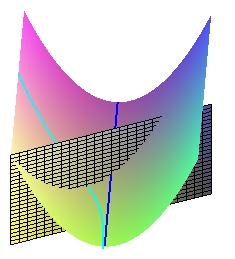
Les géographes définissent le talweg comme la "ligne joignant les plus bas points des sections transversales successives d'une vallée" ; mais qu'est-ce qu'une section transversale ? La figure ci-contre montre que le point le plus bas de la section par un plan vertical d'une gouttière pentue n'est pas forcément au centre de cette gouttière, lieu intuitif du talweg (en bleu foncé) ; pire encore, la ligne de pente (en bleu clair) passant par le point le plus bas est orthogonale au plan. Cette orthogonalité ne permet donc pas de reconnaître le talweg... La section transversale doit être orthogonale au talweg... Donc pour définir la section transversale, il faut déjà le connaître ! La définition géographique ne peut donc être prise comme définition mathématique.

Voici un série de définitions qui ont été proposées, dont on verra qu'elles ont toutes leurs limites ; lorsque les lignes définies ci-dessous traversent des régions convexes, ce sont des lignes de crête, et lorsqu'elles traversent des régions concaves, ce sont des lignes de talweg (les points de la surface sont dits "convexes" quand la section de la surface par un plan vertical tangent à la ligne de niveau y présente un maximum d'altitude, "concaves" quand elle y présente un minimum). Par réflexion horizontale, les lignes de crête et de talweg s'échangent.
 
 

Première définition (proposée par Jordan en 1872, reprise par Dieudonné dans son calcul infinitésimal par exemple et utilisée par les topographes de l'IGN) : les lignes de crête et de talweg d'une surface sont les lignes de pente aboutissant à un col ; ligne de crête pour la partie montante en partant du col, ligne de talweg pour la partie descendante. Cette définition est non soutenable pour au moins trois raisons : 1 : pour une surface non bornée comme la gouttière ci-dessus, il peut y avoir une vallée, mais aucun col ! 2 :  on peut toujours localement modifier la surface de sorte qu'une ligne de pente donnée aboutisse à un col (ou l'inverse) et pourrait donc devenir faîte ou talweg, ou ne plus l'être ; voir aussi le texte de Boussinesq ci-dessous. 3 : une ligne de pente partant d'un col peut très bien devenir asymptote à une autre (cf exemple ci-contre) : on obtient alors une vallée ayant plusieurs talwegs distincts !

Deuxième définition (proposée par de Saint Venant en 1852, reprise par exemple dans le dictionnaire de mathématiques de F. Le Lionnais et celui d'A. Warusfel, acceptée comme définition mathématique actuellement).
Une direction verticale étant choisie, les lignes de crête et de talweg sont les lignes tracées sur la surface joignant les points où la pente (de la section de la surface par un plan vertical tangent à la ligne de pente) présente un minimum le long de la ligne de niveau correspondante. Autrement dit, ce sont les lignes de déclivité minimale.

Cette définition formalise l'idée que le talweg est moins pentu que les lignes de pente voisines qui le rejoignent (et de même la crête est moins pentue que les lignes de pente voisines qui s'en éloignent).

Cependant les lignes rejoignent en fait les points d'inflexion de lignes de pente (en projection horizontale), et ne sont donc des lignes de pente que lorsque leur projection horizontale est rectligne.
 

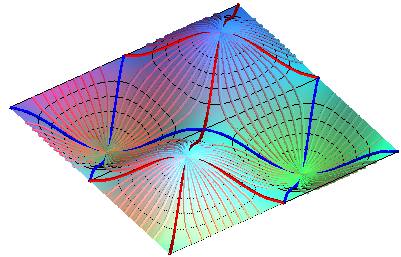
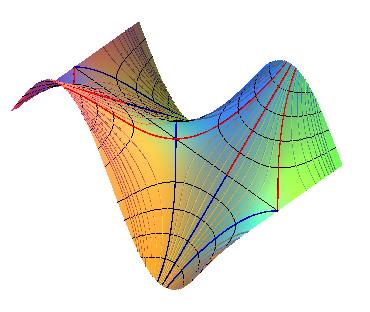
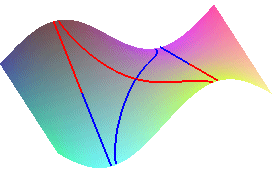
Exemple : Vue des crêtes (en rouge) et talwegs (en bleu foncé) de la surface z = y sin x qui sont obtenus avec cette définition, (plus quelques lignes de pente, en bleu clair) ; on remarque que les crêtes et talwegs qui aboutissent au col ne sont pas des lignes de plus grande pente, et ne correspondent pas aux crêtes et talwegs intuitifs tracés à droite !

 

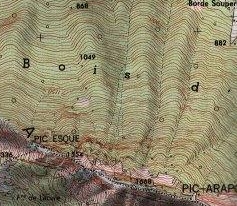
Troisième définition, par la courbure horizontale maximale, proposée par Gauch en 1993. Une direction verticale étant choisie, les lignes de crête et de talweg sont les lignes tracée sur la surface joignant les points où la courbure horizontale (donc celle de la ligne de niveau passant le point) de la ligne de niveau y présente un maximum. Cette définition est motivée par le fait que sur les cartes topographiques, les lignes de niveau présentent en général un coude au niveau des crêtes et talwegs, comme ci-contre.

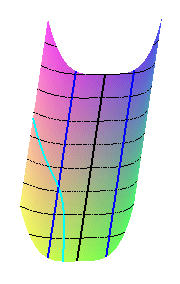
La courbure horizontale, dont il faut déterminer les maximums, vaut :   (son signe détermine la concavité du point - positif pour convexe, négatif pour concave). Malheureusement, pour la surface z = y – x^4, en forme de vallée en U, la définition 3 donne, en plus de la droite centrale, qui correspond intuitivement au talweg géographique, deux droites parallèles (qui ne sont pas des lignes de pente), ce qui ferait 3 talwegs pour une vallée ! Pire encore, pour la surface z = y – rac(1-x^2), dont les courbes de niveau sont des arcs de cercle, tout point est extrémum de courbure, donc les talwegs recouvriraient toute la vallée !

z = y - x^4 : (Faux) talwegs en bleu foncé, lignes de niveau en noir, de pente, en bleu ciel, talweg normal en noir gras.

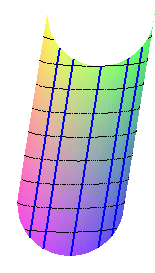z = y - rac(1-x^2) : avec la def 3 tous les points de la vallée seraient points de talweg !

Quatrième définition (proposée par Boussinesq en 1872 - voir ci-dessous et reprise en partie dans le dictionnaire de mathématiques de F. Le Lionnais)

Les lignes de crête et de talweg sont les lignes de pente dont les lignes voisines se rapprochent lorsqu'on les parcourt dans le sens de la pente (talweg), ou s'éloignent (crête).
Définition non soutenable car toute ligne de pente d'une surface non plane serait crête ou talweg !

Cinquième définition (proposée par Rothe en 1915).
Les lignes de crête et de talweg sont les lignes de pente singulières, en ce sens qu'elles correspondent aux solutions singulières de l'équation différentielle des projections horizontales des lignes de pente.
 

Avec les notations de Monge, l'équation différentielle des lignes de pente de la surface z = f(x,y) étant qdx - pdy = 0, les lignes de crête et de talweg sont formées de l'ensemble des points où u est nul ou non défini, u étant un facteur intégrant de qdx - pdy : u(qdx - pdy) = dF. Par exemple pour la surface z = y sin x , qdx - pdy= sinx dx - y cos x dy  et  d F = d (exp(x²) cos²x)= -2 exp(y²)cosx (qdx - pdy). Les solutions singulières sont données par u = 0, soit cos x = 0 soit  x = pi/2 + kpi. Cette définition a le défaut de ne pas être géométrique et de ne pas forcément fournir les lignes de pente partant d'un col ...

Sixème définition :
Les lignes de talweg et de crête sont les lignes de pente qui sont aussi lignes de courbure de la surface (lignes tangente à une direction principale, ou la courbure est extrémale).
On démontre que ces lignes correspondent aux lignes de pentes dont la projection sur un plan horizontal est rectiligne, déjà obtenues par la définition 2.

En résumé, il n'y a consensus que pour les lignes de pente à projection rectiligne !

Exemples :
- les lignes de faîte et de talweg d'une surface de révolution d'axe vertical sont les méridiennes (si l'on prend la définition au sens large ; au sens strict, il n'y en a pas)
- les lignes de faîte et de talweg d'un cône de direction verticale sont les génératrices coupant orthogonalement les lignes de niveau (pour un cône , cela correspond aux extremums de f).
 
 

Note de M. J. Boussinesq présentée en 1872 à l'Académie des Sciences. Dans une Note du 3 juin 1872 (Comptes rendus, t. LXXIV, P. 1458), .Y. C. Jordan a essayé de définir géométriquement les faîtes et les thalwegs, lignes que tout le monde reconnaît à la surface du sol et pourrait y tracer à fort peu près, mais dont on éprouve quelque peine à dégager le caractère précis. M. Jordan pense : 1° que ces lignes ne se distinguent en rien, dans leur parcours, des autres lignes de plus grande pente; 2° que leur seul caractère particulier se trouve en leur point de départ, les noms de faîte et de thalweg devant être réservés exclusivement aux lignes de plus grande pente, au nombre de quatre, qui se détachent d'un col, et dont deux (faîtes) s’élèvent à partir de ce point, tandis que les deux autres (thalwegs) vont au contraire en s'abaissant. On voudra bien me permettre d'observer que ces deux propositions me paraissent, la seconde trop restrictive, et la première en désaccord avec la notion des faîtes et des thalwegs, telle qu'elle se trouve, plus ou moins nette, dans tous les esprits. Les thalwegs et les faîtes se distinguent en effet, sur leur parcours, des autres lignes de plus grande pente; car l'habitant des montagnes sait fort bien tracer, avec toute la précision possible, le thalweg de sa vallée ou le faîte qui sépare le versant qu’il habite du versant voisin, sans avoir besoin de se transporter à l'origine, souvent très éloignée et presque inaccessible, de ces lignes, et d'observer les circonstances, bien peu importantes, que la configuration du sol peut y présenter. D'ailleurs, si l'existence des mêmes lignes tenait à celle des cols, la plupart des vallées, qui n'ont point de col à leur origine, mais dont la partie supérieure est une sorte d'amphithéâtre s’appuyant sur la crête d'une montagne, n'auraient point de thalweg, et les diverses vallées qui rayonnent tout autour d'un sommet ne seraient séparées les unes des autres par aucune ligne de faite; conséquences évidemment inadmissibles. Pour obtenir le vrai caractère des faîtes et des thalwegs, il convient de considérer d'abord ces lignes dans le cas où elles sont le plus visibles, c’est-à-dire lorsqu'elles se trouvent marquées par l'intervention, saillante ou rentrante, de deux parties du sol à pentes opposées et qui se coupent sous un angle dièdre différent de 180 degrés. On voit alors qu’une ligne de plus grande pente, prolongée supérieurement jusqu’à un faîte y change brusquement de direction, et se confond, au-dessus, avec le faîte  lui-même; et aussi, que, prolongée inférieurement jusqu’à un thalweg, elle y offre un autre point anguleux, pour se confondre, plus bas, avec le thalweg lui-même. Un faîte est donc comme une artère d’où se distribuent à droite et à gauche et sur toute sa longueur, en descendant, une infinité de lignes de plus grande pente ordinaires, pareilles aux vaisseaux capillaires qu'on étudie en anatomie ; tandis qu'un thalweg est comme une veine qui reçoit de droite et de gauche, sur tout son parcours, les lignes de plus grande pente ordinaire. Ce caractère est modifié, mais reste très reconnaissable quand, en vue d'avoir une surface continue, on substitue dans le même cas, aux parties anguleuses du sol, d'autres parties arrondies qui s'en écartent extrêmement peu ; alors les lignes de plus grande pente présentent, aux endroits où elles se rapprochent de celles de faîte ou de thalweg, un petit arc à très grande courbure au lieu d'un point anguleux, et elles tendent ensuite rapidement à se confondre avec ces lignes, dont elles sont bientôt à des distances tout à fait imperceptibles ; à ce moment, leur réunion physique au faîte ou au thalweg est complètement effectuée, bien que, au point de vue abstrait ou géométrique, elles continuent asymptotiquement à monter à côté du faîte ou à descendre à côté du thalweg, jusqu'à l'extrémité supérieure du premier ou à l'extrémité inférieure du second, et il en est de même, à cela près que la direction des lignes de plus grande pente varie plus graduellement d'un point à l'autre, quand la surface du sol n'a que de petites courbures, tout en affectant néanmoins, comme il arrive presque partout par suite de l'action des eaux, la forme de sillons juxtaposés. Dans tous ces cas, le sol est divisé en bandes allongées, ou versants dont chacun est le lieu géométrique d'une série de lignes de plus grande pente contiguës l'une à l’autre sur toute leur longueur, et qui, le coupant transversalement, se détachent de son bord supérieur, appelé sa ligne de faîte, pour aboutir à son bord  inférieur, appelé sa ligne de thalweg. En résumé, une ligne de faîte est une ligne de laquelle se détachent, sur tout son parcours, des lignes de plus grande pente qui en étaient d'abord à des distances nulles ou imperceptible et qui s’en éloignent à des distances notables ; un thalweg est une ligne à laquelle, sur tous les points de son parcours, viennent se réunir, en toute rigueur, ou du moins asymptotiquement, des lignes de plus grande pente qui en étaient d'abord à des distances sensibles ; tel est le caractère qui distingue ces lignes remarquables de celles de plus grande pente ordinaires, qui sont au contraire, sur tout leur parcours contiguës à leurs voisines.

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2020