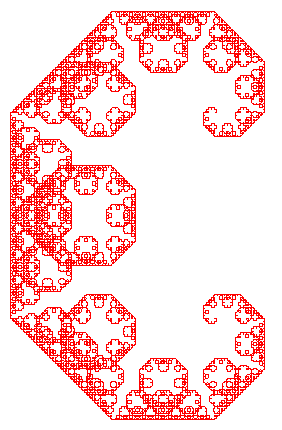
C curve (or Levy's curve), C-Kurve (oder Levysche Kurve)
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
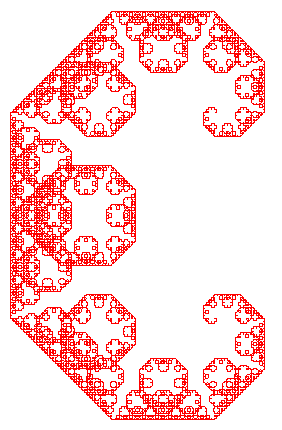 |
COURBE DU C (ou COURBE DE LÉVY)
C curve (or Levy's curve), C-Kurve (oder Levysche Kurve) |
| Courbe étudiée par Paul Lévy en
1938.
Paul Lévy (1886 - 1971) : mathématicien français. Autre nom : dragon de Lévy. |
La courbe du C est l'attracteur
dans le plan de deux similitudes directes de centres distincts A
et B, de rapport
et d’angles
; sa dimension fractale est donc
; on montre que sa dimension est exactement 2, mais que sa frontière
a pour dimension environ 1,9340.
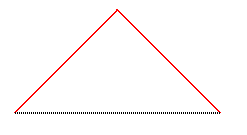
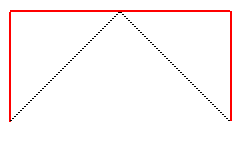
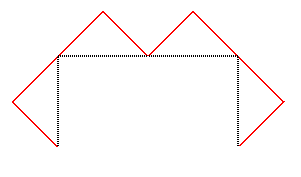
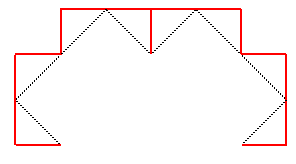
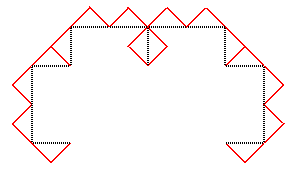
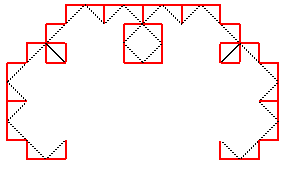
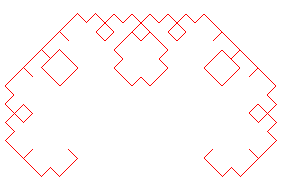
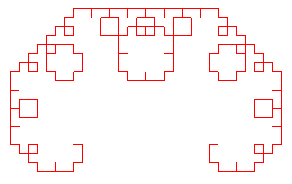
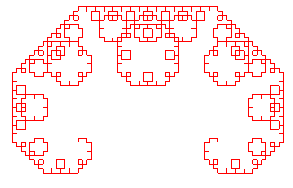
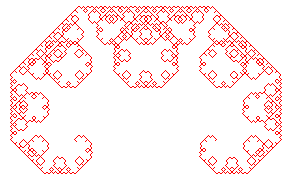
Voici la suite des compacts convergeant vers cette courbe,
en partant de [AB] :
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

Vue illustrant les deux similitudes internes
Regarder aussi l'arbre dont la courbe du C est le feuillage, et la définition de la courbe du C par L-système.
La courbe du C est la réunion quasi disjointe de deux copies d'elle-même ; il y a exactement six figures du plan ayant cette propriété.
Comme sa cousine la courbe
du dragon, la courbe du C pave
le plan.
Variantes :
Si l'on considère un triangle (ABC) isocèle
rectangle en C, soit f une isométrie qui transforme [AB]
en [AC] et g une isométrie qui transforme [AB] en [CB] ;
suivant la nature de f et g, on obtient, comme attracteur
de f et g, les diverses courbes suivantes :
| A et B ont pour images respectives par f | A et B ont pour images respectives par g | de plus | Courbe associée |
| A et C | C et B | f et g sont directes | Courbe du C |
| A et C | B et C | f et g sont directes | Courbe du dragon |
| C et A | B et C | f et g sont directes | Courbe de Césaro
(pour les étapes paires) |
| A et C | B et C | f et g sont indirectes | Courbe de Polya |
Ci-dessous le dessin original de Paul Lévy paru dans son article de 1938.
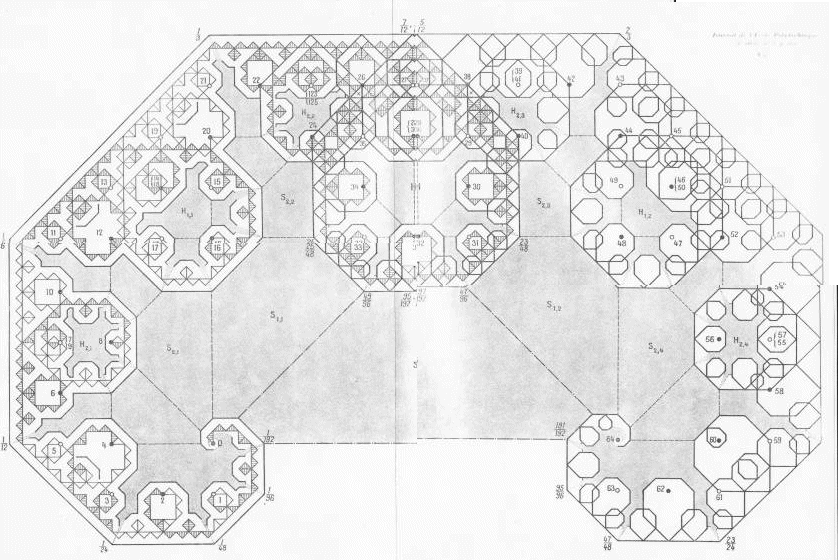
Personnellement, j'aurais plutôt baptisé la courbe du C la "courbe du crabe", regardez :

| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2010