Une courbe remplissante en dimension n est une courbe paramétrée continue à valeurs dans  dont l'image a une mesure n-dimensionnelle non nulle (une aire non nulle en dimension 2, un volume non nul en dimension 3) ; c'est le cas des courbes fractales ayant une dimension fractale entière.

Voici la construction d'une courbe remplissant un compact K de  supposé réunion de p compacts  semblables à K numérotés de telle sorte que chaque compact touche le suivant.

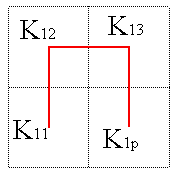(figure avec un carré, mais ceci vaut pour un compact quelconque)

On partage maintenant chacun de ces compacts en p compacts toujours semblables à K ce qui donne p² compacts  numérotés de sorte que les p premiers recouvrent  les p suivants recouvrent  etc.., et les p derniers recouvrent  et de sorte que chaque compact touche toujours le suivant.

  compacts   deux compacts successifs se rencontrant, recouvrant successivement les compacts .

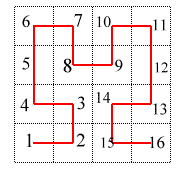
Si t appartient à [0,1[ , posons  (où [ t] désigne la partie entière de t).

Les  , pour t fixé, forment alors une suite de compacts emboîtés dont l’aire tend vers 0 ; leur intersection est donc réduite à un point  ; la courbe paramétrée  est uniformément continue et se prolonge en une courbe  , courbe de type Peano remplissant entièrement le compact K.

La courbe de type Peano correspondant à cette construction, approchée à l'ordre n est la ligne brisée joignant les centres de gravité successifs des compacts  ; elle converge au sens de Hausdorff vers la courbe de type Peano.
 

Dans le cas d'un carré partagé en 4 carrés, on obtient les courbes de type Peano binaires, avec comme cas particuliers la courbe de Hilbert, ou la courbe de Moore. La courbe de Lebesgue est obtenue par le même principe de base, mais avec une astuce supplémentaire la rendant différentiable presque partout.

Dans le cas d'un carré partagé en 9 carrés on obtient les courbes de type Peano ternaires ; lorsque les carrés sont parcourus par un balayage continu aller-retour, on obtient une courbe souvent appelée "la" courbe de Peano dans la littérature, car celui-ci en avait donné la paramétrisation dans son article de 1890 (mais la figure se trouvant dans cet article est celle de la courbe désignée maintenant par courbe de Hilbert ; Peano connaissait donc déjà bien cette dernière courbe ; il n'a détaillé la courbe ternaire que parce que les calculs sont plus simples dans ce cas).

Dans le cas d'un triangle rectangle isocèle coupé en deux triangles homothétiques, on obtient la courbe de Cesàro, dont 4 exemplaires donnent la courbe de Sierpinski.

Dans le cas d'un triangle isocèle évidé du triangle central, on obtient la courbe triangulaire de Sierpinski, qui remplit le tamis de Sierpinski.

Dans le cas d'un cube partagé en 8 cubes, on obtient la courbe de Hilbert 3D.

Voir aussi la courbe de Gosper, qui remplit l'île du même nom,  le terdragon et le terpapillon.

Il n'existe pas de courbe remplissante différentiable (partout).
 
 

fractal suivant

fractal précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2026