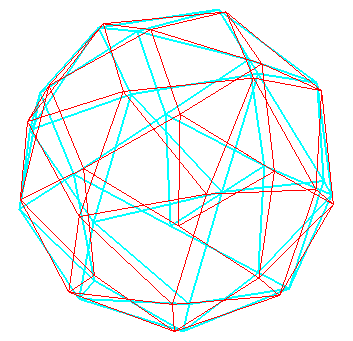
Anaglype à regarder avec des lunettes rouge (à gauche) et bleu (à droite)
Programme Maple de tracé.
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CUBE ADOUCI
Snub cube, abgeschrägter Würfel
.
Anaglype à regarder avec des lunettes rouge (à gauche) et bleu (à droite) Programme Maple de tracé. |
| Autre nom : cube camus. |
| Famille | polyèdre semi-régulier ou polyèdre d'Archimède | ||||||
| Historique | solide connu d'Archimède (IIIe s. av. J.C.) | ||||||
| Autre nom | cube camus | ||||||
| Dual | icositétraèdre pentagonal | ||||||
| Faces | 32 triangles et 6 carrés | ||||||
| Sommets | 24 sommets de degré 5, de code de Schläfli 34.4 | ||||||
| Arêtes | 60 arêtes de longueur a ;
angle dièdre entre un carré et un triangle entre deux triangles : Remarque : le cube adouci n'est donc pas constructible à la rêgle et au compas. |
||||||
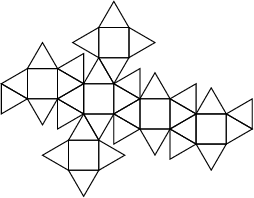
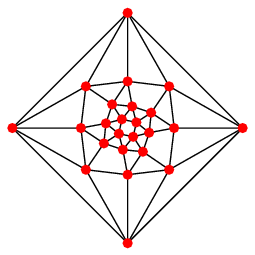
| Patron et graphe |
 ( ( |
||||||
| Diamètres | sphère inscrite dans les carrés : intersphère (tangente aux arêtes) : |
||||||
| Mensurations | volume : coefficient isopérimétrique : |
||||||
| Coordonnées des sommets | Permutations paires de |
||||||
| Construction | adoucissement du
cube
ou de l'octaèdre
 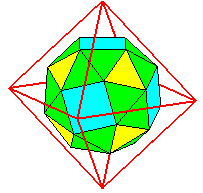
Les carrés jaunes sont obtenus à partir d'une face du cube par similitude directe de rapport Voir sur cette page une excellente animation de la construction. Remarquons qu'on passe du rhombicuboctaèdre au cube adouci en "partageant" les carrés verts en deux triangles : 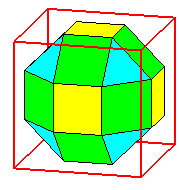 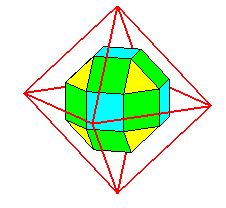 |
||||||
| Plans de symétrie | Aucun ; le cube adouci est donc "chiral" : voir les 2 versions ci-dessus. | ||||||
| Axes de rotation |
|
||||||
| Groupe des isométries | = groupe des rotations du cube ou de l'octaèdre (pas d'isométrie négative). | ||||||
| Remarque | Contrairement à ce qui se passe pour les polyèdres semi-réguliers non "adoucis", le groupe des isométrie n'agit pas transitivement sur les faces de même type. |
 |
Le problème des dictateurs ennemis consiste à
se demander comment sont disposées sur une sphère
n
calottes sphériques identiques (les empires de chaque dictateur)
de taille maximale et ne se chevauchant pas.
Dans le cas n = 24, il a été démontré que la réponse optimale consiste à disposer les dictateurs aux sommets d'un cube adouci. Sources : Marcel Berger, Pour la Science n° 176, p. 72 et Dossier Pour la Science n° 41 p. 40. |
Voir aussi le dodécaèdre
adouci.
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2008