Un polyèdre (P*) est dit dual (combinatoire) d'un polyèdre (P) s'il existe deux bijections de l'ensemble des sommets de l'un vers l'ensemble des faces de l'autre telles que deux sommets reliés par une arête de l'un aient pour images deux faces adjacentes de l'autre.
(P*) a donc autant d'arêtes que (P) et les nombres de sommets et de faces s'échangent.

Voici une définition ensembliste équivalente : si (P) est un polyèdre, notons E(P) le treillis formé de l'ensemble vide, des singletons sommets de P, des arêtes de P (considérées comme paires de sommets), des faces de P (considérées comme ensembles de sommets) et de l'ensemble des sommets de (P).
Deux polyèdres (P) et (P*) sont alors combinatoirement duaux s'il existe une bijection de E(P) dans E(P*) envoyant les arêtes de l'un sur celles de l'autre, les sommets de l'un sur les faces de l'autre, et qui renverse les inclusions (l'existence d'une bijection conservant les inclusions signifiant l'équivalence combinatoire des polyèdres). Un dual d'un dual est donc un polyèdre équivalent au polyèdre de départ.
 
 

Une première méthode pour déterminer un dual d'un polyèdre est de choisir un point sur chaque face, et de relier par une arête chaque paire de points situés sur des faces contigües ; chaque face du dual est alors bordée par les arêtes déterminées par les points choisis sur les faces aboutissant à un même sommet du polyèdre de départ ; il faut pour cela que ces arêtes soient coplanaires et que donc les points choisis sur toutes les faces aboutissant à un même sommet soient toujours coplanaires ; ceci est réalisé si les sommets du polyèdre de départ sont de degré 3, ou si le polyèdre est régulier, en choisissant sur chaque face le centre de celle-ci. Cette méthode est un cas limite du chanfreinage, quand le rapport d'homothétie k vaut 0.

Une deuxième méthode, valable pour tout polyèdre convexe utilise la polarité par rapport à une sphère :

Considérons une polarité (ou dualité) par rapport à une sphère centrée en un point intérieur au polyèdre (P) ; à tout sommet du polyèdre de départ correspond par cette polarité un plan qui contiendra une face du polyèdre dual polaire (P*), les sommets de cette face étant les points images par la dualité des plans contenant les faces qui aboutissent au sommet de départ (dans le même ordre).

Lorsque le polyèdre de départ est convexe et que le centre de la sphère de polarité est à l'intérieur du polyèdre, alors le dual polaire est un polyèdre convexe (donc tout polyèdre simple étant équivalent à un polyèdre convexe, pour tout polyèdre simple il existe un polyèdre simple dual combinatoire de ce polyèdre) ; dans les autres cas, le polyèdre obtenu par polarité peut être étoilé.


Exemple :
• polyèdre de départ : le cube (convexe) délimité par les plans d'équations cartésiennes :
x = 1 ; x = -1 ; y = 1 ; y = -1 ; z = 1 ; z = 3 ;
• sphère de polarité : la sphère de centre O et de rayon 1 ;
• polyèdre dual polaire : l'octaèdre non-convexe de sommets de coordonnées cartésiennes :
(1,0,0) ; (-1,0,0) ; (0,1,0) ; (0,-1,0) ; (0,0,1) ; (0,0,1/3) ;

Voir ici (pdf), ou ici (word) un problème présentant les propriétés de la polarité par rapport à une sphère.
 

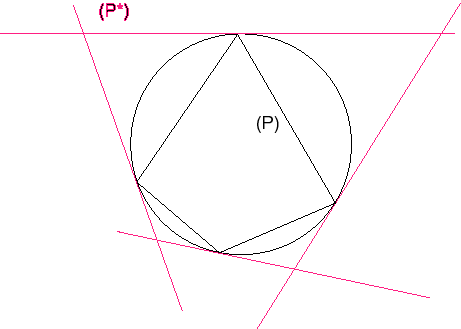
Les plans contenant les faces du dual polaire (P*) d'un polyèdre inscriptible (P) obtenu par polarité par rapport à la sphère circonscrite sont tout simplement les plans tangents à la sphère passant par les sommets de (P) ; inversement, les sommets du dual d'un polyèdre circonscriptible sont les points de tangence avec la sphère inscrite. Par exemple, les sommets du dual d'un polyèdre régulier obtenu par polarité par rapport à la sphère inscrite sont les centres de gravité de chaque face.

Les arêtes de (P) sont orthogonales aux arêtes du dual polaire ; si donc le polyèdre possède une sphère tangente à chaque arête, les arêtes du dual sont les perpendiculaires en chaque point de tangence aux arêtes de (P).

D'un point de vue pratique, la polarité par rapport à la sphère d'équation  échange le point de coordonnées  et le plan d'équation  ; si donc A,B,C sont trois sommets consécutifs d'une face de (P) le sommet de (P*) correspondant à cette face est  (voir ce texte pour plus de détails).

Voici les figures des duaux des polyèdres réguliers obtenus par polarité par rapport à leur sphère circonscrite :

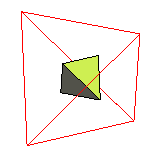
tétraèdre (autodual)

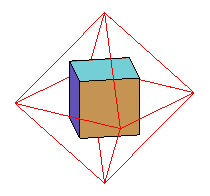
cube et octaèdre

dodécaèdre et icosaèdre

D'une façon générale, les pyramides sont auto-duales, les prismes et diamants s'échangent par dualité, ainsi que les antiprismes et antidiamants.

Voici les figures des duaux des 13 polyèdres archimédiens obtenus par polarité par rapport à leur intersphère, formant la famille des polyèdres de Catalan :

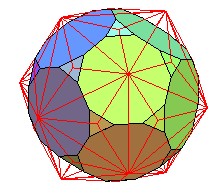
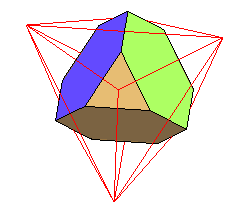
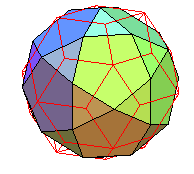
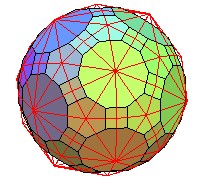
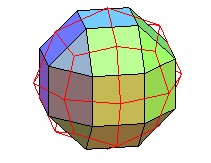
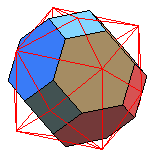
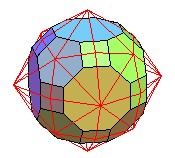
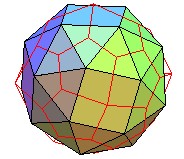
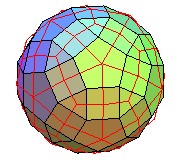
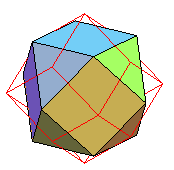
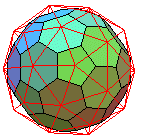
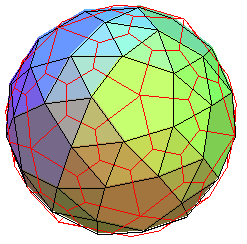
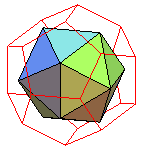
Pour finir, le superbe dual du pentaki-dodécaèdre;adouci :
 

dual du pentaki-dodécaèdre-adouci

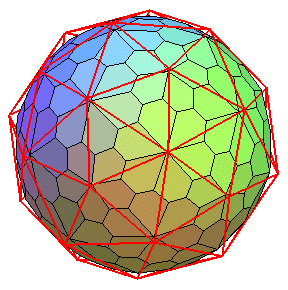
le même, avec en rouge le pentaki-dodécaèdre

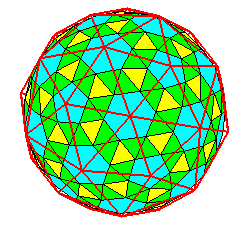
le pentaki-dodécaèdre adouci, avec en rouge le pentaki-dodécaèdre

Voir plus généralement le dual d'un polytope.
 
 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2005