Voir aussi : fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Cauchy_(g%C3%A9om%C3%A9trie) www.apmep.fr/IMG/pdf/APM1.pdf http://www.polyhedra-world.nc/poly_news.htm demonstrations.wolfram.com/SteffensFlexiblePolyhedron/ smf.emath.fr/files/imported/Publications/ExplosionDesMathematiques/pdf/smf-smai_explo-maths_23-27.pdf Vidéo de micmaths

Un polyèdre est dit flexible si on peut le déformer continûment, chacune de ses faces restant identique à elle-même durant la déformation (imaginer que le polyèdre est formé de plaques rigides articulées suivant les arêtes), rigide ou indéformable dans le cas contraire. Un polyèdre flexible est appelé un flexaèdre.

Cauchy a démontré en 1813 que tout polyèdre convexe est rigide ; il a même démontré que si deux polyèdres convexes sont combinatoirement équivalents, et que les faces correspondantes sont isométriques, ils sont alors congruents (i.e. image l'un de l'autre par une isométrie de l'espace).
 

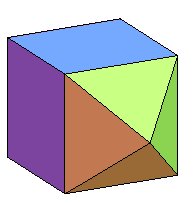
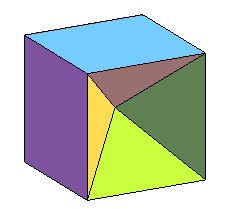
Ce dernier théorème est clairement faux pour les polyèdres quelconques, même sans trou, comme le montrent les deux polyèdres ci-contre, qui sont bien équivalents à faces isométriques, mais non congruents.

 

Les deux polyèdres précédents sont cependant chacun rigide ; En 1897, Bricard a fabriqué un "octaèdre" flexible, mais ce n'est pas un vrai polyèdre car les faces se recoupent. Ce n'est qu'en 1977 qu'un vrai flexaèdre a été construit par Robert Connelly, simplifié ensuite en un polyèdre à 9 sommets par Klaus Steffen (ci-contre). On ne sait pas s'il existe un flexaèdre à 8 sommets.

Un autre problème de rigidité est celui concernant les polyèdres à arêtes articulées aux sommets.
Dans ce cas, le tétraèdre et l'octaèdre sont rigides, mais, par exemple, le cube est mobile ; cependant, Cauchy a démontré que tout polyèdre à arêtes articulées convexe à faces triangulaires est rigide ; voir cette page.
 
 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2014