angle dièdre 164° 53' 17"
icosaèdre sur les faces duquel sont posées 20 pointes à 6 pans ou bien dodécaèdre sur les faces duquel sont posées 12 pointes à 10 pans.
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
HEXAKI-ICOSAÈDRE
Hexakis icosahedron, Hexakisikosaeder
| Famille | polyèdre semi-régulier de deuxième espèce, polyèdre de Catalan |
| Historique | étudié par Catalan en 1862 |
| Etymologie | du grec "hexakis" six fois + "icosaèdre" (les faces de l'icosaèdre ont été partagées en 6) ; il pourrait aussi s'appeler le décaki-dodécaèdre... |
| Autre nom | hexa-icosaèdre, en anglais : disdyakis triacontahedron |
| Dual | icosidodécaèdre tronqué |
| Faces | 120 triangles d'angles 32,8°, 58,2° et 89,0°. |
| Sommets | 62 : 30 sommets de degré 4, de code de Schläfli 34, 20 sommets de degré 6, de code 36, et 12 de degré 10 de code 310 |
| Arêtes | 180 : 60 arêtes de longueur a , 60 de longueur
0,64 a , 60 de longueur 1,18 a
angle dièdre 164° 53' 17" |
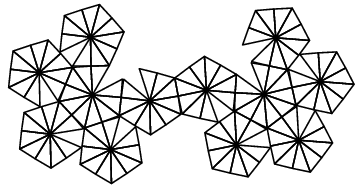
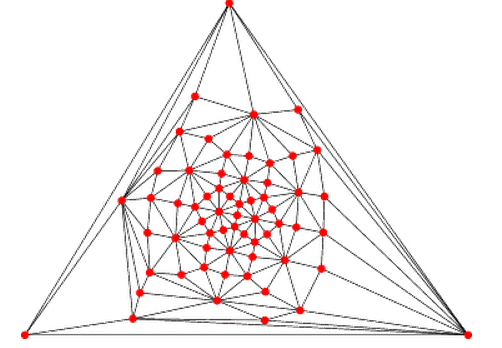
| Patron et graphe |
  |
| Diamètres | sphère inscrite : 3,41 a ; sphère circonscrite : 3,77 a |
| Mensurations | volume : 30,81 a3 ; aire : 54,16 a² |
| Constructions | Dual polaire de l'icosidodécaèdre
tronqué
icosaèdre sur les faces duquel sont posées 20 pointes à 6 pans ou bien dodécaèdre sur les faces duquel sont posées 12 pointes à 10 pans. |
| Groupe des isométries | = celui de l'icosaèdre |
 Alain Esculier Alain Esculier |
 |
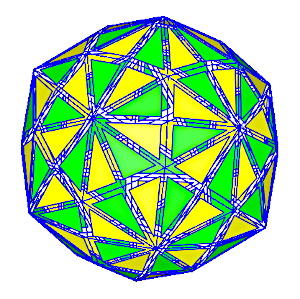 |
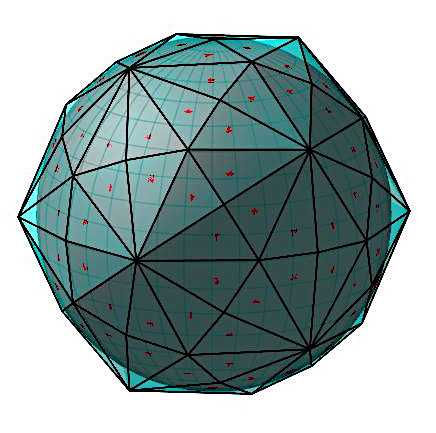
| L'hexaki-icosaèdre et sa sphère inscrite.
Bien remarquer les sommets de degré 10, centres des pentagones du dodécaèdre sous-jacent, et les sommets de degré 6, centres des triangles de l'icosaèdre sous-jacent. |
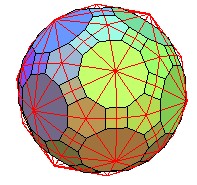
Pavage sphérique associé. | L'hexaki-icosaèdre est 2-coloriable. |
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2020