Un hyperprisme de dimension n est un polytope de dimension n ayant deux hyperfaces (ses bases) translatées l'une de l'autre, et dont les sommets correspondants sont joints par des arêtes (les deux bases étant situées dans deux hyperplans strictement parallèles) ; les k-cellules de l'hyperprisme sont les k-cellules des bases, plus, pour tout couple de  (k–1)-cellules homologues des deux bases, le k-prisme de bases ces (k–1)-cellules. Les cellules qui ne sont pas dans la base sont appelées les cellules latérales de l'hyperprisme.

Par exemple, un hyperprisme de dimension 4 résulte de la translation d'un polyèdre dans la quatrième dimension. Ses cellules latérales sont les prismes joignant deux faces homologues des deux polyèdres. Ses faces latérales sont les parallélogrammes joignant deux arêtes homologues.

La mesure d'un hyperprisme est le produit de la mesure d'une de ses bases par la distance entre les deux hyperplans contenant les bases.

Les hyperprismes dont toutes les cellules sont elles-mêmes des hyperprismes sont les parallélotopes, qui sont de n façons différentes un hyperprisme (prendre les n couples d'hyperfaces symétriques).
C'est en particulier le cas de l'hypercube de dimension n qui est aussi le seul hyperprisme à être un polytope régulier. Mais on désigne en général par hyperprisme régulier un hyperprisme dont les bases sont des polytopes réguliers et la translation entre les bases se faisant perpendiculairement à celles-ci. Toutes les k-cellules latérales sont alors des hyperprismes réguliers isométriques entre eux.

Exemple :
 

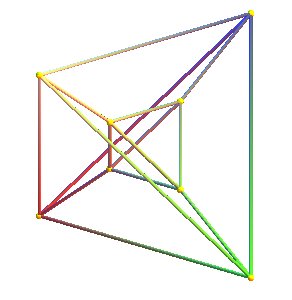
Perspective conique plane d'un prisme régulier à bases triangulaires : les arêtes parallèles deviennent concourantes, mais en 3D, le prisme a deux faces triangulaires et 3 faces carrées.	Perspective conique 3D d'un hyperprisme de dimension 4 régulier à bases tétraédriques ; en 4D l'hyperprisme a deux cellules tétraédriques et 4 cellules prismatiques à bases triangulaires, 8 faces triangulaires et 6 faces carrées.

Comparer avec les hyperpyramides.
 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2015