Du grec prisma "prisme", provenant du verbe prizein "scier".

Un antiprisme d'ordre n (ou n-gonal) est un polyèdre ayant deux faces (ses bases) à n côtés, chacun des sommets de l'une étant joint par deux arêtes à deux sommets de l'autre, formant ainsi 2n  faces latérales triangulaires.
 

Les antiprismes et les antidiamants s'échangent par dualité.

L'antiprisme est dit droit s'il est à symétrie de rotation d'ordre n.
 

Le seul antiprisme qui soit un polyèdre régulier est l'octaèdre (cas n = 3) et il l'est de 4 façons différentes. D'autre part, il y a, pour un ordre donné, un seul antiprisme à faces latérales régulières. Les antiprismes à faces latérales régulières sont semi-réguliers.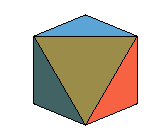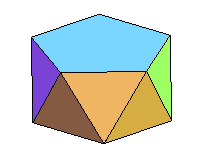

antiprismes semi-réguliers d'ordres 3, 4 et 5.

Carte de visite de l'antiprisme droit d'ordre n :

Faces	2n triangles équilatéraux et deux n-gones réguliers.
Sommets	2n sommets de degré 4.
Arêtes	4n arêtes, 2n d'un type, 2n d'un autre.
Coordonnées  des sommets	, avec  pour l'antiprisme semi-régulier.
Faces correspondantes

Formules :
 
 

Le cosinus de l'angle dièdre vaut , ce qui donne en degrés, pour n allant de 3 à 6 : 109,4712207, 127,5516029, 138,1896843, 145,2218914

 
 
 
 

Le problème des dictateurs ennemis consiste à se demander comment sont disposées sur une sphère n calottes sphériques identiques (les empires de chaque dicateur) de taille maximale et ne se chevauchant pas. Dans le cas n = 8 , on pourrait penser qu'il suffit de mettre les dictateurs aux sommets d'un cube, mais la bonne réponse est donnée par les sommets de l'antiprisme d'ordre 4 à faces régulières. Sources : Marcel Berger, pour la Science 176, p. 72 et dossier Pour la Science 41 p. 40.

Généralisation : antiprisme à faces croisées
Voir aussi les prismes.
 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2018