

cube
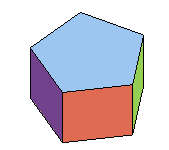
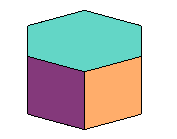
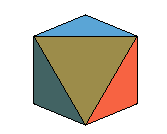
octaèdre
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
POLYÈDRE SEMI-RÉGULIER
Semi-regular polyhedron, halbregulares Polyeder
| Autre appellation : polyèdre isogonal. |
Un polyèdre semi-régulier (de première
espèce) est un
polyèdre
à faces régulières et "sommets-transitif", c'est-à-dire,
tel que pour tout couple de sommets, il existe une isométrie de
l'espace conservant globalement le polyèdre et transformant un sommet
en l'autre. Autrement dit, le groupe des isométries du polyèdre
agit transitivement sur l'ensemble des sommets.
Plus concrètement, cela se traduit par le fait
que si l'on fabrique une boîte moulant entièrement le polyèdre,
le polyèdre pourra toujours y être rangé en plaçant
l'un des sommets au hasard (attention, les angles des faces arrivant à
un sommet ne sont par contre pas forcément égaux, il faudra
peut-être tourner le polyèdre sur lui-même pour qu'il
s'encastre).
Cette définition implique les propriétés
suivantes :
Un polyèdre semi-régulier est convexe,
inscriptible
(existence d'un point équidistant des sommets) et
- concernant les faces :
1) toutes
les faces sont régulières (il est donc IFR
et CFR)
- concernant les sommets :
2a) tous les
sommets ont même degré
2b) les angles
solides aux sommets sont tous égaux
2c) les figures
de sommets (formées par les demi-droites issues du sommet) sont
deux à deux isométriques.
- concernant les arêtes
3) toutes
les arêtes ont même longueur
Une condition nécessaire et "quasi"- suffisante pour qu'un polyèdre soit semi-régulier est
1) d'être convexe
à faces régulières
2) d'avoir des figures de sommets
(formées par les demi-droites issues de chaque sommet) deux à
deux isométriques.
3) d'être inscriptible
Un seul polyèdre vérifie ces 3 propriétés
sans être semi-régulier : le gyro-rhombicuboctaèdre.
Il existe deux familles infinies de polyèdres semi-réguliers : les prismes et les antiprismes à faces régulières et exactement 16 autres polyèdres semi-réguliers, à isométries près : les 3 polyèdres réguliers de Platon restants (le cube étant un prisme et l'octaèdre un antiprisme), et les 13 polyèdres d'Archimède.
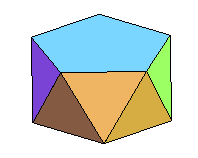
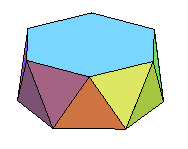
Voici les premiers prismes et antiprismes semi-réguliers :
 |

cube |
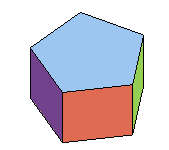 |
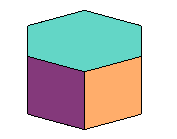 |

octaèdre |
 |
 |
 |
La même définition s'applique aussi aux polyèdres
étoilés, auquel cas on remplace souvent l'appellation
"semi-régulier" par "uniforme".
Il existe deux familles infinies de polyèdres
semi-réguliers étoilés : les prismes
et les antiprismes étoilés
à faces régulières et exactement 57 autres polyèdres
étoilés semi-réguliers, à isométries
près : les 4 polyèdres de Kepler-Poinsot
, et les 53 polyèdres de
Badoureau-Coxeter.
Voir aussi les polyèdres semi-réguliers
de seconde espèce.
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2016