Spherical equation: , pour . Cartesian parametrization: . Volume: . Attraction of the homogeneous solid with density  and mass M on a massive point with mass m located at O: .

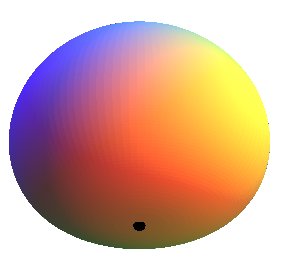
Given a massive point, the surface of equal attraction is the locus of the points contributing with the same given intensity to the (Newtonian) attraction force applied to the massive point, such force resulting from the various attraction forces of the whole surface.

Proof: If Oz is the direction of the resulting force, and the attracted massive point is located at O, then the component of the attraction of a point with spherical coordinates  ( = longitude,  = latitude) is proportional to , hence the equation  of the surface.

It is the surface of revolution obtained by rotation of a half curve of the dipole (or curve of equal attraction) around its symmetry axis.

It can be proved that the homogeneous solid with mass M such that the (intensity of the) attraction applied to a given massive point is maximal among all the solids with mass M, or solid of maximal attraction, is the solid encompassed by this surface.
 
 

Comparison between the attractions of this solid (Smax) and of a sphere with same volume and same density:
Radius of the spherical ball with same volume as (Smax): . Attraction of this ball applied to a point placed on its surface: . Ratio of the attractions: : (Smax) wins by a short head...

 
 

Proof of the maximality of this solid, given by Bertrand in 1864 (see this book page 430, and see also this book page 45). Since the attraction of a body on a massive point is always, according to previous statements, of finite intensity, we can look for the shape of a homogeneous body with given mass, for which its attraction on a given molecule would be the maximum possible. First, it is obvious that the attracting body must contain the attracted molecule, because otherwise, a portion could be detached from this mass and transported in contact with the attracted point, so that its action is applied in the same direction as the resulting action of all the other portions while increasing it more than it could have in its initial position. It can also be noted that two molecules with the same mass, both located on the surface of the attracting body, must apply on the attracted point actions the components of which, in the direction of the total resulting action, are equal. Otherwise, the resulting action could be increased by transporting the molecule with the smaller component onto the other one, with changing the global attracting mass. The solid of maximal attraction is therefore delimited by the surface of equal attraction.

 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017