CROSS-CAP
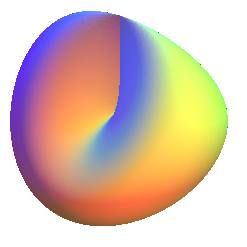
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CROSS-CAP
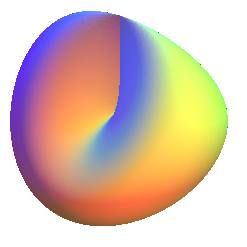
| Surface studied by Steiner???
Other name: mitre. |
Cartesian parametrization #1: 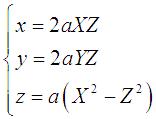 with
with Cartesian parametrization #2: Cartesian parametrization #3: Cartesian parametrization #4: |
The cross-cap is the image of the quotient sphere with
antipodal points identified (i.e. the real
projective plane), by the map: .
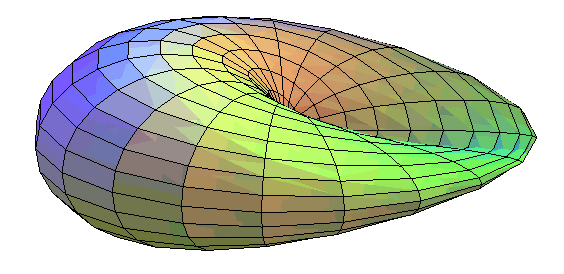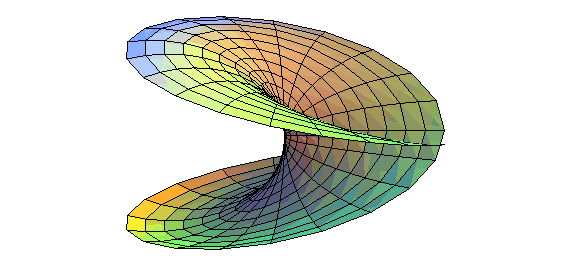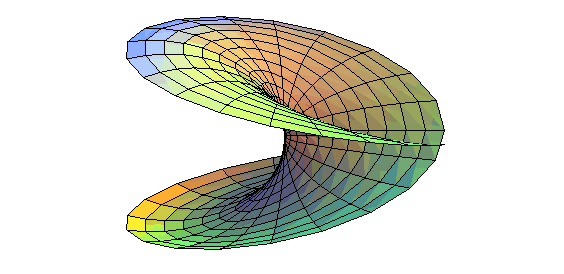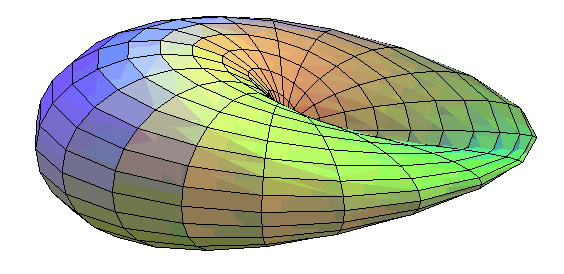
| The cross-cap is one of the simplest immersions
of the real projective plane
into It has only one segment line of self-intersection that ends with two cuspidal points (here O and (0, 0, a)) (compare to the Roman surface and the Boy surface, which are two other immersions of the projective plane). |
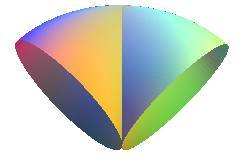 |
| The figure opposite illustrates the fact that the cross-cap is a model of the projective plane: |
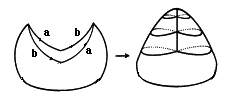 Start with a holed sphere (homeomorphic to the disk), and stick edge to edge a with a and b with b, to form the segment line of self-intersection |
| Another construction, starting from a disk with its edge twisted to a figure-eight, with already a self-intersection. |
 |
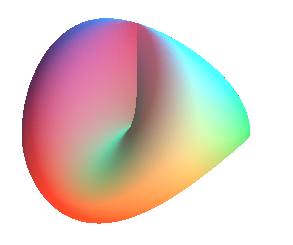 .
It is then really a cap in the physical sense, but from a topological point
of view, it is a Möbius strip.
.
It is then really a cap in the physical sense, but from a topological point
of view, it is a Möbius strip.
The cross-cap also has interesting geometrical properties. In particular, it is a reunion of a family of ellipses, in three different ways:
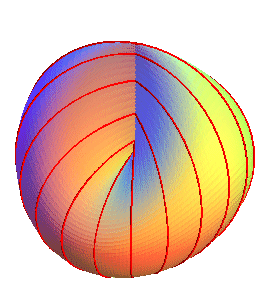
| First family (cf. parametrization
#2: the sections by the planes containing Oz
with polar angle q are the ellipses,
with secondary vertices (0, 0, a) and |
 |
||
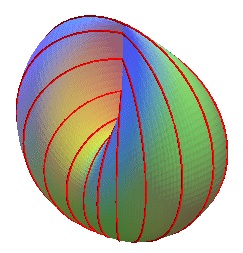
| If the previous ellipses are replaced by circles, we
get a circled surface with cylindrical
parametrization: This latter surface, homeomorphic to the previous one, is the image by inversion of the Plücker conoid of order 1, the lines of the conoid becoming the circles of this cross-cap. |
 |
||
| Second family (cf. parametrization
#3): the sections by the planes containing Oy In blue, the locus of the vertices. |
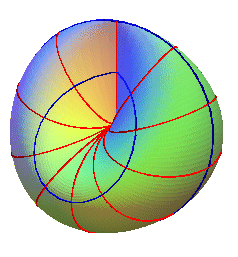 |
||
| Third family (cf. parametrization
#4): the sections by the planes |
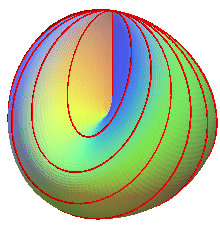 |
||
|
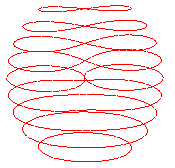 |
| Here is a polyhedral version of the cross-cap.
Be careful, this is not a true polyhedron: the double central edge is common to 4 faces. |
 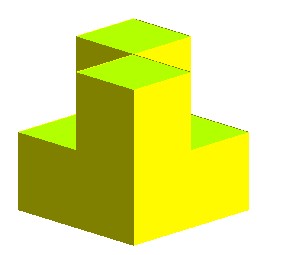 |
The cross-cap must not be mistaken for the pseudo cross-cap:

| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017