
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
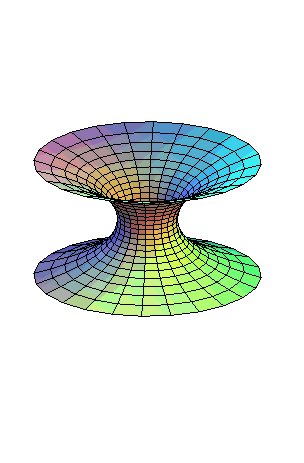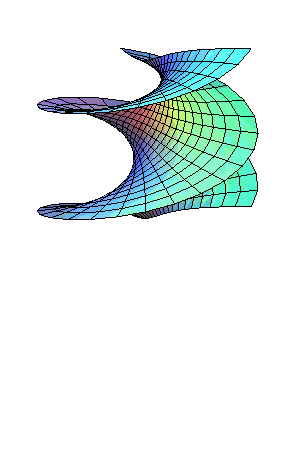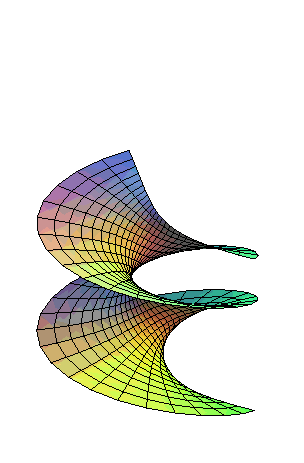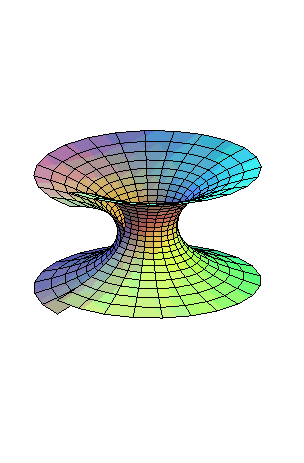
CATENOID
 |
 |
 |
| Surface studied by Euler in 1740.
The name comes from catena: chain, which is also the Latin name of the catenary. Other name: alysseid, from the Greek alusion "small chain" (given by Bour in 1862). |
| Cylindrical equation: Cartesian parametrization: Parametrization for which the coordinate lines are the rhumb lines forming an angle First fundamental quadratic form: where Surface element: Second fundamental quadratic form: Gaussian curvature: Area of the portion Volume: |
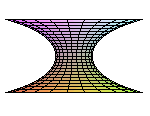
The catenoid is the surface of revolution generated by the rotation of a catenary around its base.
We get the parametrization
by taking
and
in
the Weierstrass parametrization
of a minimal surface.
| Consider two parallel circular rings with diameters D
at distance d;
It can be proved that if d/D < 0.66, there exist 3 minimal surfaces supported by these two rings: 2 catenoids and the so-called Goldschmidt surface, composed of the two disks delimited by the rings. It can be proved that if d/D < 0.53, the surface with minimal area between these 3 is one of the 2 catenoids (in red opposite); but starting from 0.53, it is weirdly the Goldschmidt surface which has minimal area. And starting from 0.66, it is the only surface anyway: there no longer are catenoids supported by the rings. Remarks:
|

Animation showing the profile of the 2 catenoids for d/D ranging from 0.1 to 0.66; |
On this picture, the theoretical limit 0.53 of blow-up seems to be exceeded
by far...
|
| A catenoid can be continuously and isometrically transformed
into a right helicoid,
the surface remaining constantly minimal.
Equations of this transform: The intermediate surfaces are the minimal helicoids. |
 |
See also the skew catenoid,
the trinoid, and the
axial revolution of the catenary.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2019