Ludwig Schläfli (1814-1895): Swiss mathematician.

A double six is a set of 12 lines in the 3-dimensional projective space, often written, the notation being due to Schläfli, as a matrix:

The number 6 is the maximal value of n such that a set of 2n lines can have this property (proof of this fact).

To construct a double six, we can start from a line  with 5 secants  such than none of them is included in the quadric generated by 3 of the 4 other lines.
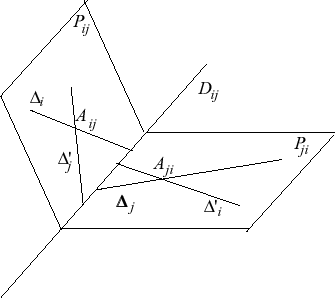
Four lines among the 5 secants  admit  as a common secant and also have another common secant: if {i, j, k, l, m}={1, 2, 3, 4, 5}, write  the common secant to  different from ; it can be proved that  does not intersect with : to finish this double six, we just need the line : common secant to  that does not intersect with : the (difficult) double six theorem states that such a line exists.

Every line of the double six cuts exactly 5 others; therefore, there are  intersection points in the double six.
 

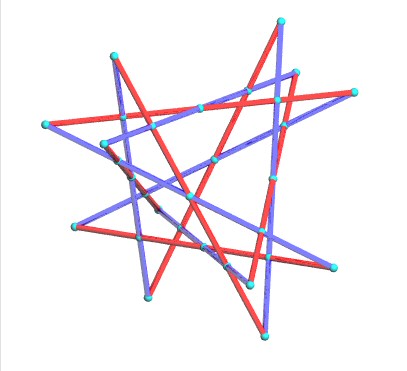
The 30 pairs of secant lines  generate 30 planes , and the 15 pairs of planes  are composed of planes that intersect along 15 lines .

 
 

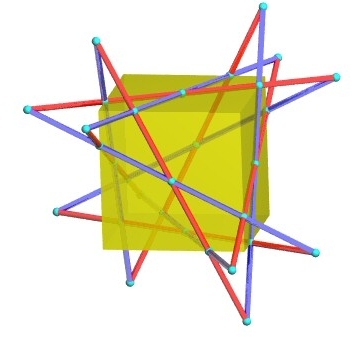
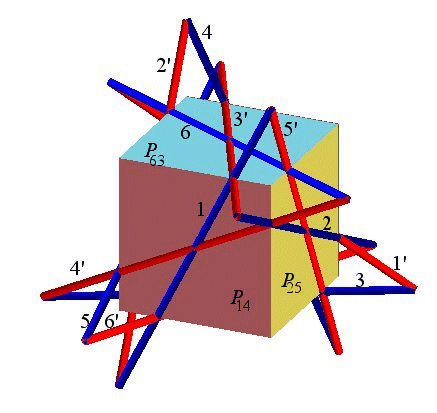Figure of the double six with the six lines  in blue (written i alone to simplify), and the six lines  (written i') in red;  Every red line cuts exactly 5 blue lines and vice versa. This affine view was chosen in order for the 6 planes  , ,  to be the 6 faces of a cube. This way, the 3 lines  are the 3 lines at infinity of the faces of the cube.

 
 

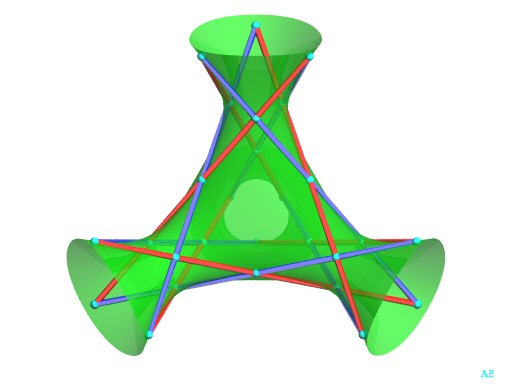	There exists a unique smooth cubic surface (S) containing the 12 lines of the double six. For the double six represented above, where the vertices of the chosen cube are  etc, and the line  passes by , the equation of the cubic surface is: .
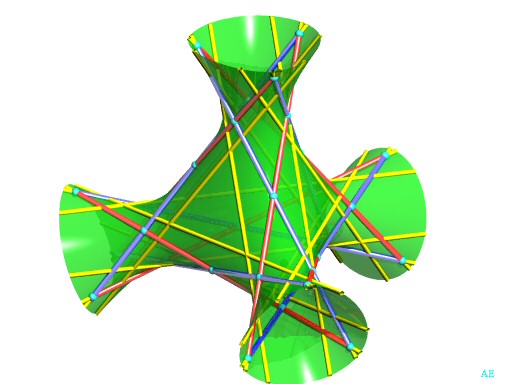	The 27 lines of this cubic are the 12 lines of the double six (in red and blue opposite) plus the 15 lines (in yellow) defined above. (but remember that in the representation opposite, the 3 lines  are the 3 lines at infinity of the faces of the cube and therefore there are only 12 visible yellow lines)

The figure composed of the 27 lines is called eikosiheptagram (eikosihepta = 27 in Greek).
In this setting, every line intersects with exactly ten others:
    - every yellow line  is secant to the 4 red and blue lines  and with the  yellow lines  for (proof of this fact).
    - every red line  is secant to the 5 blue lines  and the 5 yellow lines .
Therefore, there exist  pairs of non secant lines.

It can be proved that there exist, in the eikosiheptagram, exactly 36 double sixes:
    - the initial double six N.
    - the  double sixes of the type , qualified as "syzygetic" to N
    - the  double sixes of the type , qualified as "azygetic" to N.

The group of the permutations of the 27 lines that respect the incidences of the lines therefore has 6 ! . 2 . 36 = 51 840 elements; it is isomorphic to the Weyl group W(E₆) and its subgroup of even permutations is isomorphic to the symplectic projective group PSp₄(F₃) which is not simple.

Each of the 30 plans  contains 3 lines of the surface (S) ( and ): they are called tritangent planes (since they are tangent to the surface at 3 points).

But there exist  other tritangent planes, coming from the above double sixes, generated by the 15 trios of two by two secant lines ; it can be proved that these 45 tritangent planes are the only ones: every line is common to 5 tritangent planes.

The incidences of the various elements of the eikosiheptagram are summarized in the table below:
 

....intersections	points	lines	tritangent planes	double six	eikosiheptagram
each point...	1	2	1	8	1
each line...	10	10	5	16	1
each tritangent plane...	3	3	15	36	1
each double six...	30	12	45	36	1
the eikosiheptagram...	135	27	45	36	1

 

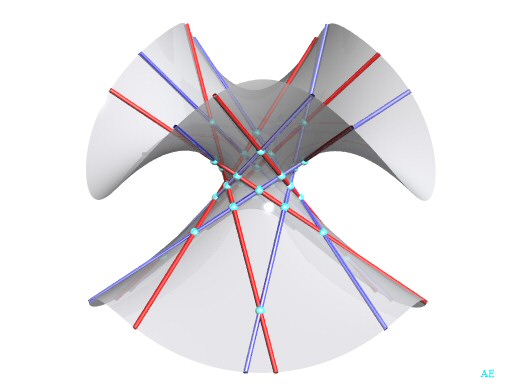Here is a view of the principal double six of the Clebsch surface.

 

This only appears to be a double six: every blue line intersects with 5 red lines, but also the sixth, at infinity! In a true double six, there cannot be more than 3 lines of each family on a same quadric (see this figure)

 

WEBOGRAPHY Java applet for the double six, on the same website: enriques.mathematik.uni-mainz.de/cubicsurface/background/background_frame.php3?shortname=doublesix Rod model for the double six: www.math.arizona.edu/~models/Wire_models/source/2.html

© Robert FERRÉOL , Alain ESCULIER 2017