CONOCUNEUS
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
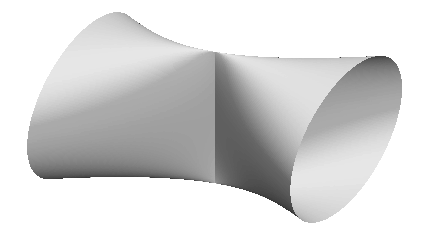
CONOCUNEUS

| Surface studied by Wallis.
Used in architecture to make a certain type of vault ("back arch of Saint-Antoine", "groin vault"...) From the Latin conus "cone", and cuneus "corner"). Other name: conical wedge. |
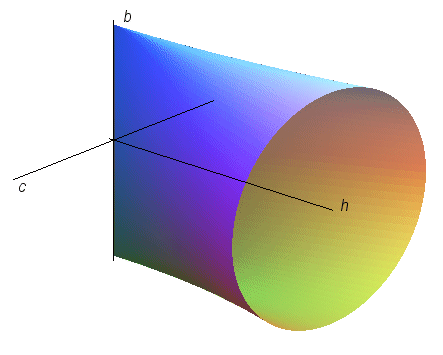
| Cartesian equation of the conocuneus with axis Oz,
directrix plane z = 0, and directrix the circle Quartic surface. Cartesian parametrization: Cylindrical equation in the case a = b: Intersection with the plane x = h: |
 |
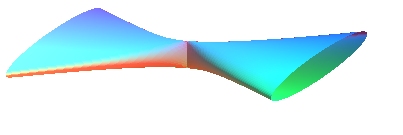
The conocuneus is the right conoid with directrix a circle parallel to the axis.
Compare to the milk carton.
See also on the page
of the general conoid the quite close case of the right conoid whose
generatrices are tangent to a sphere.
 |
 |
Casts shaped like half conocunei, made by Alexandre Demir. |
 |
 |
 |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017