Costa's surface

COSTA'S SURFACE

Surface studied by da Costa in 1982.
Celso Jose da Costa (1949-....): Brazilian mathematician.
en.wikipedia.org/wiki/Costa%27s_minimal_surface
mathworld.wolfram.com/CostaMinimalSurface.html

Gray parametrization: , ,
where refers to the Weierstrass zeta function associated to the pair (c,0) (WeierstrassZeta[z, {c, 0}] in Mathematica),
refers to the Weierstrass P function also associated to the pair (c,0)(WeierstrassP[z, {c, 0}] in Mathematica)
c and are two constants associated to the Weierstrass functions equal respectively to 189.7272... and 6.87519....

Until 1982, it was conjectured that the only complete (i.e. without boundary) non-periodic minimal surfaces without self-intersection were: the plane, the catenoid and its associated surfaces. Costa's surface, and other ones afterwards, refuted this conjecture.

It can be obtained by taking in the Weierstrass parametrization of a minimal surface: .

Costa's surface is invariant under the action of a half-turn around the axis x = y, z = 0 (in the above parametrization, y(u,v)=x(v,u) and z(v,u)=-z(u,v)), and under the action of this half-turn, the two faces are swapped.
Opposite, two half surfaces. Check that each one is the image by a half-turn of the other one

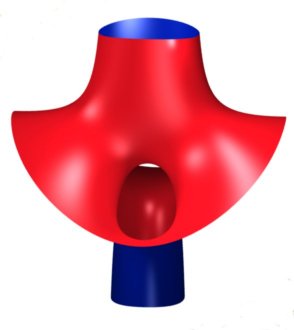
Animation of the surface the two faces of which have different colors.
Imagine water poured inside the upper funnel; it will come out by the external face of the bottom funnel...

Costa's surface is topologically equivalent to a torus minus 3 points (it is therefore of genus 1); see an animation of it here.

It is also topologically very close to the cubic algebraic surface with the very simple Cartesian equation: , which is also invariant under the action of a half-turn that swaps the two faces.
Note that the horizontal sections of the latter surface are ellipses or hyperbolas.
Note also that this surface is asymptotic for large x and y to Plücker's conoid .

Costa's surface can be generalized to a surface with order n rotational symmetry, see here.

Compare Costa's surface to the finite Riemann minimal surface, which also has a plane sheet and two flared sheets, but that intersect with each other.

Costa's surface, by Alain Esculier

Costa's surface by Patrice Jeener, with his kind authorization

next surface previous surface 2D curves 3D curves surfaces fractals polyhedra