Cushion

BOULIGAND'S PILLOW

Surface studied by Bouligand in 1928 [bouligand, geometrie analytique, pb ENS 1928, p 487].
Homemade name.

Cartesian equation of the pillow alone:

.
Cartesian equation of the whole surface, turned by an eighth of a turn with respect to the previous one:

or also

, the pillow alone being obtained for

.
Parametrization of the pillow alone:

.
Quartic surface.

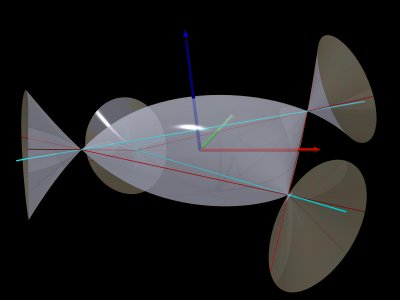
© Alain Esculier	Bouligand's pillow is the locus of the points for which the sum of the distances to two fixed perpendicular lines is constant (the two lines are the diagonals of the pillow). Remark: these pillows can be seen as the boundaries of the balls for the norm on .
	The complete surface is the locus of the points for which the sum or the difference of the distances to the two fixed lines is constant. It has 4 conical points, and 4 lines passing by them. The sections of this surface by the planes x or y = constant are ellipses or hyperbolas, the sections by the planes y = +-x are unions of parabolas, and the level curves z = constant are generalizations of cross-curves.
	Generalization: locus of the points for which the sum or the difference of the distances to any two lines is constant. We still get a quartic with 4 conical points.