Cartesian parametrization: (where ). Cartesian equation: . Rational algebraic surface of degree 9. First fundamental quadratic form: . Surface element: . Second fundamental quadratic form: . Gaussian curvature: 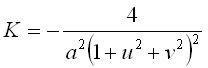. Zero mean curvature (minimal surface). Principal radii of curvature: 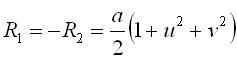. Area of the surface obtained for : . The curvature lines are the coordinate lines associated to the parametrization by u and v (and their are planar). The asymptotic lines are obtained by taking .

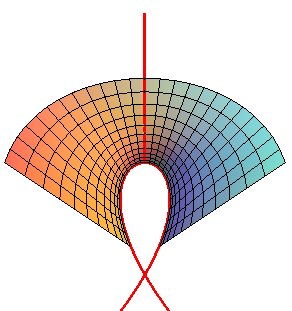
Enneper surface, represented up to the level of its self-intersection curve.

The Enneper surface is the minimal surface obtained by taking  in the Weierstrass parametrization of such surfaces: .
 
 

It can be geometrically defined as the envelope of the mediatrix planes of two points located on two homofocal parabolas (i.e. parabolas the planes of which are perpendicular and such that the vertex of one passes by the focus of the other one; compare to the definition of the symmetric parabolic Dupin cyclide). As is the configuration of homofocal parabolas, the Enneper surface is invariant under the action of a half-turn, here with axis x = y, z = 0 (swap u and v in the parametrization) which swaps the two faces of the surface.  In the opposite figure, notice that the two faces, the red and the blue, are identical. See also Costa's surface, that has the same property.

 

As the formulas  show, the projections on xOy of the lines r = constant are hypotrochoids with parameter q = 4; in particular for , we get a quatrefoil. The 3D curves r = constant are seam lines of tennis balls.
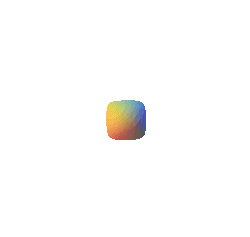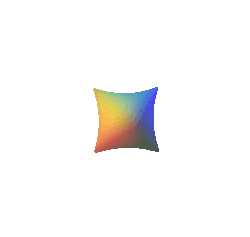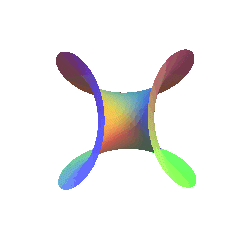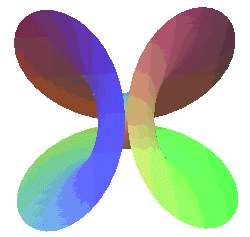Therefore, an Enneper surface can theoretically be materialized by soaking the seam line of a tennis ball  into a soapy solution in order to obtain a thin layer of soap.	Made with povray by Alain Esculier

Yet, there exist two other minimal surface supported on the same edge, symmetric images of one another, with a smaller area than that of the Enneper surface.  These two surfaces are intermediaries between the two cylinders supported on the edge and represented opposite, and the Enneper surface.
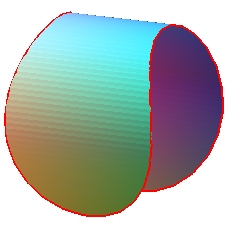A physical layer of soap assumes the shape of one of these two surfaces and not that of the Enneper surface; besides, a simple jolt makes the shape go from one surface to the other.	Picture by Alain Esculier

 

The two sections of the Enneper surface by its symmetry planes (obtained by taking u = 0 and v =0 in the parametrization) are Tschirnhausen cubics. They are geodesics, which is why the Enneper surface is a Björling surface associated to a Tschirnhausen cubic (minimal surface for which this cubic is a geodesic).

 

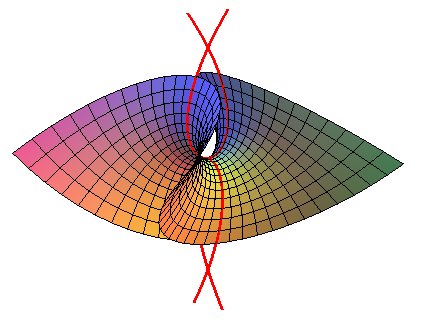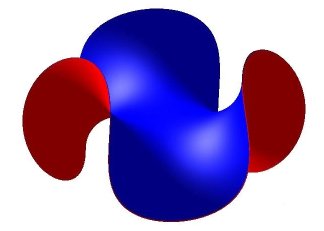
If we take  in the Weierstrass parametrization, we get the Enneper surface of ordern, parametrized by:  The classic Enneper surface is obtained for n = 2, and the case n = 3/2 gives the Bour surface. The projections on xOy of the lines r = constant are hypotrochoids with parameter q = 2n, and these lines are, up to scaling, Capareda curves.

Case n = 3 (cf the monkey saddle)

Case n = 5

Compare to the Scherk surface, another minimal surface.
 

Ice sculpture of the Enneper surface of order 3.

Engraving of the Enneper surface, by Patrice Jeener, with his kind authorization.

Enneper surface chair

Enneper surface of order 2 by Alain Esculier

Enneper surface of order 4 by Alain Esculier

 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017