A cell decomposition of a finite type manifold of dimension n (i.e. a topological space locally homeomorphic to a closed ball of  and that is the finite union of parts homeomorphic to such balls) is a finite partition of this surface is subsets homeomorphic to  for p n.

If we write  the number of subsets homeomorphic to , it can be proved that the number:  does not depend on the cell decomposition; it is called Euler characteristic of the manifold. It is a topological invariant.

The Euler characteristic is additive under disjoint union: the characteristic of a manifold that is the disjoint union of two manifolds is the sum of the characteristics of these two manifolds.

Examples:

The characteristic of  and of all its open balls is  (1 for the point, –1 for the line or an open subset, 1 for the plane or an open disk , –1 for  and its open balls ).

The characteristic of  (sphere of ) , union of a copy of  and a point, is (–1)ⁿ + 1 (0 for the circle or any Jordan curve, 2 for the sphere and all the surfaces that are homeomorphic to it).

The characteristic of a closed ball non reduced to a point of  (union of a closed ball and a copy of ) is 1; this holds in particular for a segment line or a closed disk).

The characteristic of the cylinder (plane + line) is zero, thus so is that of the cylinder with one or two boundaries, of the Möbius strip (be it closed or open), of the torus and of the Klein bottle.

The characteristic of the projective plane is 1 (open Möbius strip plus a point).

The Euler characteristic of a connected sum of two surfaces is given by the relation  (loss of two open disks); this way we get the characteristic of any closed surface.

It is equal to 2 – 2n for the n-torus and 2 – n for the sphere with n cross-caps: .

More generally, the characteristic of the sphere with p holes, q cross-caps and punctured r times (in the shape of an open or closed disk) is equal to ; this provides the characteristic of any connected surface of finite type.

Two orientable (resp. non orientable) connected surfaces with the same number of boundaries are homeomorphic if and only if they have the same characteristic.

The Euler characteristic of a surface of finite type can be computed in several ways.

A cell decomposition of the surface is here a finite partition of this surface in subsets homeomorphic to the plane (the F faces), to the line (the E edges), or to the point (the V vertices) and the Euler characteristic is computed thanks to the formula.
 

For the sphere, c = V - E+ F = 2 - 4 + 4  = 2.

For the torus, c = V - E + F= 4 - 8 + 4 = 0.

For the projective plane, c = V  - E + F= 3 - 6 + 4  = 1. (The double edge must be counted twice)

But the Euler characteristic can also be computed by the mountain dweller relation: if the surface is immersed in R³ and the altitude function has a finite number of singularities which are the v valleys, t tops and s saddles, then the Euler characteristic is .
 

For the sphere, c = v - s + t = 1 - 0 + 1  = 2.

For the torus, c = v - s + t = 1 - 2 + 1 = 0.

For the projective plane, c = v - s + t = 1 - 0 + 0  = 1.

For the Klein bottle, c = v - s + t = 1 - 1 + 0  = 0.

It is also equal to the sum of the indices of the singularities of a vector field with a finite number of singularities traced on the surface (Hopf theorem).
 
 

For the sphere, 2 singularities of index 1, or one singularity of index 2: c = 2.

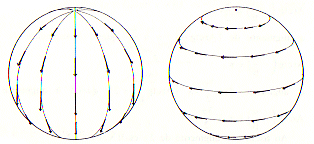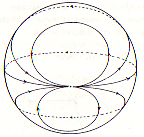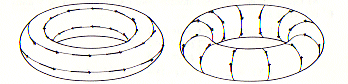
For the torus, no singularity: c = 0.

 

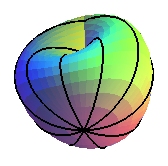
For the projective plane, one singularity of index 1 c  = 1.

For the Klein bottle, no singularity: c  = 0.

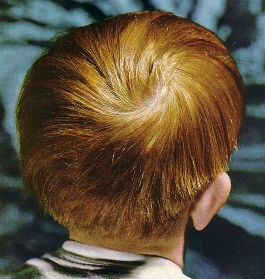
A vector field on a surface with nonzero characteristic therefore has at least one singularity; for example, a hairy ball cannot be combed without singularities.

Finally, the Euler characteristic can be computed thanks to the Gauss-Bonnet formula.

A map traced on the surface is a cell decomposition such that at least three edges reach each vertex; the chromatic number C of a surface of finite type is the minimal number of colors needed to color the faces of a map so that no two faces with at least a common edge have the same color; this number is greater than or equal to the number K, maximum number of faces of a map the faces of which all have, 2 by 2, a common edge.
By writing that, for a map, , we get, thanks to the Euler formula, the inequality  , which gives, for a map with K faces adjacent 2 by 2 and therefore having E = K (K – 1)/2 edges and verifiing V = F = K, the inequality , hence  (Heawood number).
It was proved that, with the surprising exception of the Klein bottle, these three numbers C, K and H(c), satisfying a priori , are in fact equal:
 

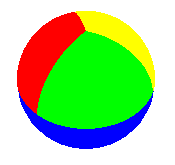
Map with K = 4 countries adjacent 2 by 2 on the sphere

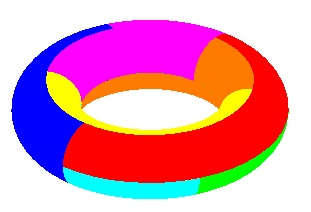
Map with K = 7 countries adjacent 2 by 2 on the torus

Map with K = 6 countries adjacent 2 by 2 on the projective plane

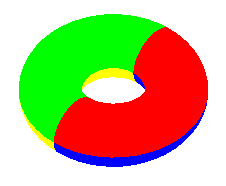
Map with K = 6 countries adjacent 2 by 2 on the Klein bottle

 
 

Surface	genus g	E. char.	Heawood number H()	chromatic number C	K
sphere	0	2	4	4	4
projective plane	1	1	6	6	6
Klein bottle	2	0	7	6	6
torus	1	0	7	7	7
Dyck's surface	3	–1	7	7	7
Klein bottle with an handle, sphere with 4 cross-caps	4	–2	8	8	8
2-torus	2	–2	8	8	8
n-torus,	n	2 – 2n
projective plane with n handles, sphere with 2n + 1 cross-caps	2n + 1	1 – 2n
Klein with n handles, sphere with 2n + 2 cross-caps	2n + 2	–2n

 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2023