| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
MORIN'S SURFACE
| Bernard
Morin (1933-2018): French mathematician.
Article of B. Morin and J.P. Petit on turning a sphere inside out: new.lutecium.org/www.jp-petit.com/science/maths_f/Retournement_sphere/PLS_79.pdf François Apery: models of the projective plane, page 104. en.wikipedia.org/wiki/Morin_surface mathinfo.unistra.fr/fileadmin/upload/IREM/Publications/L_Ouvert/n094/o_94_32-45.pdf http://www.math-art.eu/Documents/pdfs/Cagliari2013/Cagliari_Denner_Springer-009.pdf |
| François Apery's Cartesian parametrization: |
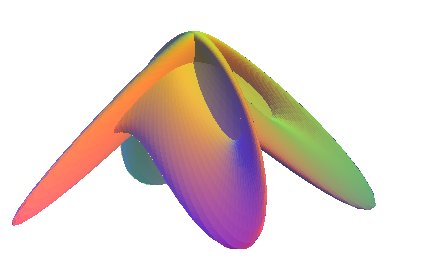
| Morin's surface is an immersion of the sphere that comes
up in the central phase of the process of turning a sphere inside out imagined
by B. Morin and J.P. Petit (cf. the above
article).
J.P. Petit's drawing opposite shows its topology. The sphere initially had a face colored in grey and a
face colored in orange. The swapping of the two faces occurs during the
central phase of the process by a simple rotation by |
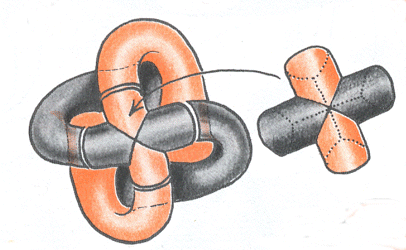 |
| For n = 2 et k = 1, the above parametrization provides a model (the case n = 3, k = 1 gives Boy's surface). |
 |
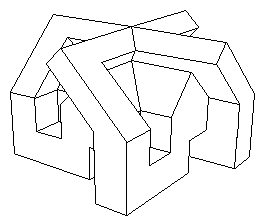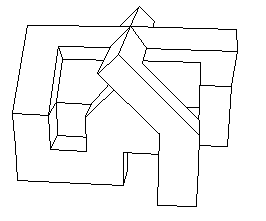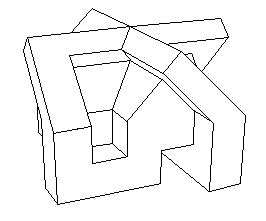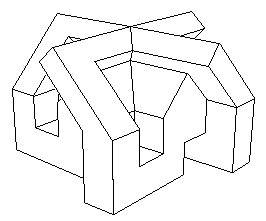
| Opposite, a polyhedral version of this surface owed to
J.P.
Petit.
Another version is owed to Richard Denner (see the links
above).
|
 |
| Apery's parametrization provides a family of surfaces with rotational symmetry of order n; opposite the case n = 5. |
 |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2017