(REAL) PROJECTIVE PLANE
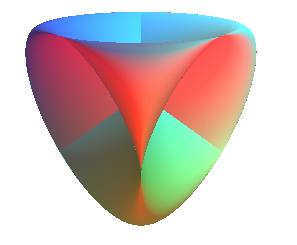
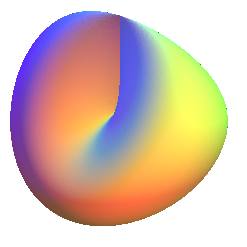

| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
(REAL) PROJECTIVE PLANE


| Surface studied by Felix Klein in 1874.
Website: www.math.ohio-state.edu/~fiedorow/math655/classification.html |
| Cartesian parametrization of an immersion in |
The (real) projective plane is the quotient space of
by the collinearity relation.
But, more generally, the notion "projective plane" refers to any topological space homeomorphic to .
It can be proved that a surface is a projective plane iff it is a one-sided (with one face) connected compact surface of genus 1 (can be cut without being split into two pieces).
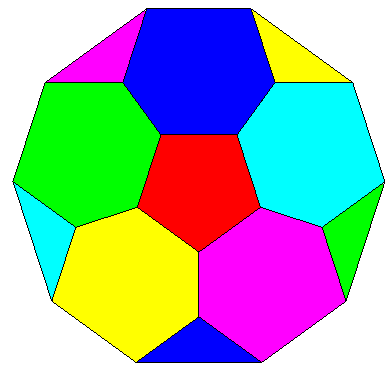
| The chromatic number of the projective plane is equal to 6 (any map traced on the projective plane can be colored with no more than 6 colors, and there exist maps that need 6 colors).
There even exist maps where each country touches the 5 others, one of which is represented opposite on the cross-cap, another one on a decagon with identified opposite sides with inversion of direction (cf. below). |
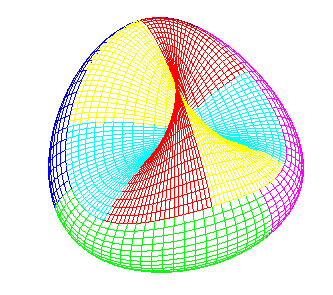 |
 |
| The three utilities problem can be solved on the projective plane, contrary to the plane. In other words, the bipartite graph The same holds for the complete graph with 5 vertices |
 |
Here are classic models of the projective plane:
- The set of vectors of with the natural topology
- A (real affine) plane completed by a projective line (line at infinity)
- A sphere where the antipodal points are identified
- A closed disk where the antipodal points of the circumference are identified
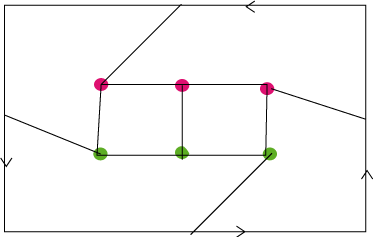
| - A closed disk two semi-circumferences of which are identified, with the indicated direction (amounts to the previous construction) | 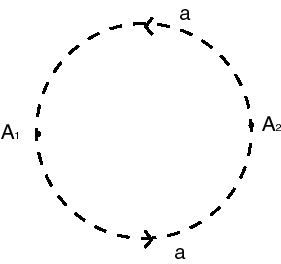 |
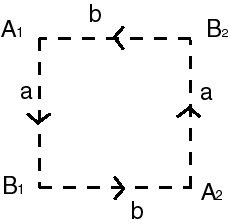
| - A full square the opposite sides of which are identified with an inversion of direction.
This amounts to the previous construction, but allows to see the link with the Möbius strip in the following characterization (the strip being obtained by identification of only one pair of opposite sides). |
 |
| - A Möbius strip the two half-edges of which are identified in opposite directions. (If they are identified in the same direction, we get a Klein bottle). |
 |
| - A Möbius strip closed by a lid homeomorphic to a disk. A Möbius strip is therefore a punctured projective plane.
To prove this start from the triangular representation of the Möbius strip and curb it. We can see the projective plane and its circular hole appear... |
|
- the star polyhedron with the same edges as the octahedron called tetrahemihexahedron.
The projective plane cannot be represented in without self-intersection; the 4 classic immersions of the projective plane in
are:
- the cross-cap (the simplest)
- the Roman surface (the first one that was historically discovered)
- Boy's surface (more complex, but without "pinch points", contrary to the first two)
- Henneberg's minimal surface, which is, additionally, a minimal surface.
The equations given in the header are those of the surfaces of obtained by immersion of the projective plane.
For , we get the cross-cap,
for , the Roman surface,
and for , we get Boy's surface (equations of Apery).
The Veronese surface is an embedding of the projective plane in .
Here are 2 constructions of the projective plane illustrated on the cross-cap.
 A Möbius strip (with self-intersection, but there is a boundary, a face) |
 + a disk (with self-intersection, but there is a boundary and two faces) |
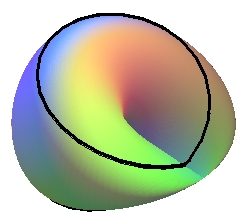
= a projective plane |
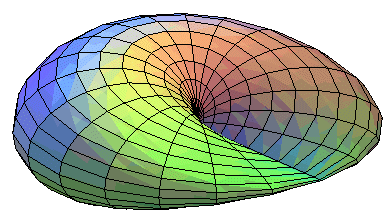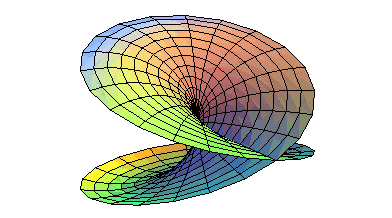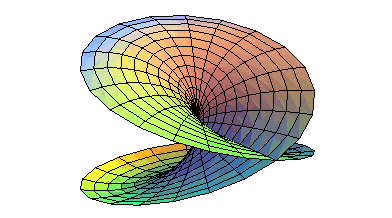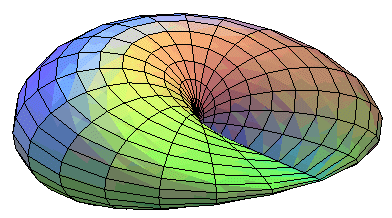
A disk can be deformed so that the points on two semi-circumferences come together: |

this... |

...is indeed equivalent to this! |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017