
n = 1

n = 2

n = 3
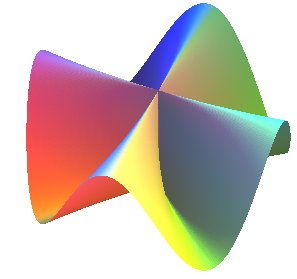
n = 4
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
PLÜCKER'S CONOID

n = 1 |

n = 2 |

n = 3 |
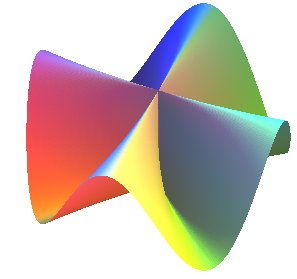
n = 4 |
| Julius Plücker (1801-1868): German mathematician
and physicist.
Other name: (Plücker's) cylindroid. See the povray programming on Alain Esculier's website. See the "exam paper" of centrale 94. |
| Cylindrical equation: Cartesian equation: Cartesian equation for an integer n: Algebraic surface rational if n = p/q is rational, of degree p + q if p is even, and 2(p + q) if p is odd. First fundamental quadratic form: Second fundamental quadratic form: Asymptotic lines: the generatrices and the curves the projections on xOy of which are are sinusoidal spirals: |
A general Plücker's conoid can be defined as a right
conoid
with directrix a cylindrical
sine wave (here, the wave )
and axis the axis of the wave.
The usual case is the case n = 2 (the directrix is a pancake curve), which is, in general, simply called Plücker's conoid:
| Cartesian equation: Rationalruled cubic surface. (remark: complete algebraic surface with equation Cylindrical equation: Cartesian parametrization: By rotation of an eighth of a turn, we get the equations: First fundamental quadratic form: Second fundamental quadratic form:
|
| Plücker's conoid has two planes of symmetry; the section by a plane parallel to a plane of symmetry is a witch of Agnesi and the section by a plane parallel to a perpendicular bisector of the planes of symmetry, an anguinea. | ||
|
See also here its invariance under the action of a half-turn.
It crosses itself along the segment line of Oz composed of the points with ordinate between -a and a, with two pinch points at the ends.
We can easily get a material representation by hollowing out a square on a sheet of paper and connecting the 4 sides of this square (construction owed to David Hanau, PCSI student).
This surface can have a lot of geometric definitions based
on the following property:
The cylinder of revolution with generatrix Oz:
cuts Plücker's conoid at an ellipse the plane of which has the equation:
,
plus the axis Oz.

Plücker's conoid is therefore also the surface generated by the common perpendiculars to a fixed line (D) = (Oz) and the lines of a fixed plane (P) non perpendicular to (D) passing by a fixed point of (P).
It is the only conoid such that for any point M, the locus of the projection of M on the generatrices of the conoid is a plane curve (which is, then, the ellipse).
Its inverse with respect to a point on the axis outside the self-intersection segment line is a cross-cap, which makes it a representation of the projective plane.
It is also projectively equivalent to Whitney's umbrella and to Zindler's conoid, but only with a complex homography for the latter.
Link
to a manipulable figure showing a Möbius strip traced on this
conoid.
 |
Construction made by the students of the architecture
school of Lyon.
It is a portion of right conoid with directrix a circle passing by the axis and forming an angle of 45° with it, therefore the image by a scaling of Plücker's conoid. Picture given by Robert March
|
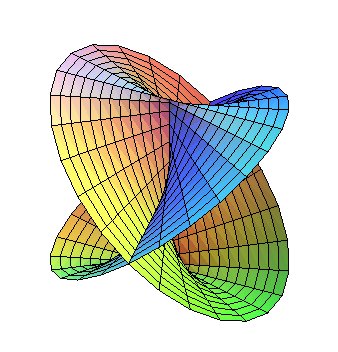
Case n = 1:
|
Cartesian parametrization: Cartesian equation: Rational ruled quartic surface. Cylindrical equation: |
 |
| The section by the cylinder Cartesian equation in this case: |
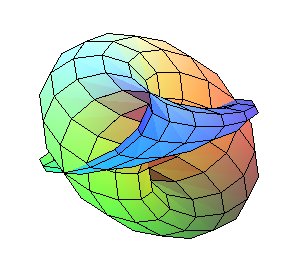 |
This conoid is the union of ellipses the vertices of which
are on the lines y = 0 and .
| It is also the locus of the tangents to the sphere with
center (a, 0, 0) and radius a, parallel to the plane
xOy,
and meeting the axis Oz. The locus of the tangency points with the
sphere is then Viviani's
curve: See the general case on the page dedicated to the conoid. |

An ellipse in blue, and Viviani's curve in red. |
| The section of this conoid |
 |
| The sections of generalized Plücker conoids More generally, the sections by the torus with center O and minor radius a are the toroidal solenoids. Opposite, two cases where n = 3. |
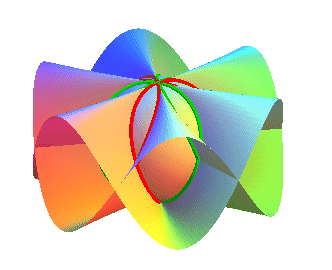 |
 |
Compare Plücker's conoids to the sinusoidal
cones.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL, Jacques MANDONNET 2017