A flippable surface is a surface globally invariant under the action of a half-turn (or axial symmetry).

A surface with Cartesian equation 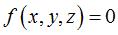 can be identified as flippable if their exists a half-turn r of  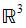such that .
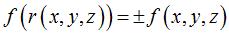With the + sign, the half-turn does not swap the two faces of the surface; examples:
    - all the surfaces of revolution
    - the ellipsoid, the centered quadrics, and more generally all the surfaces with equation 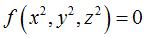 that are invariant under action of the three half-turns around the axes.
    - the cross-cap, and more generally all the surfaces with equation  that are invariant under the action of the half-turn around Oz.
 

With the - sign, the half-turn swaps the two faces of the surface; taking the axis of the half-turn to be equal to the line 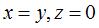 we get a general implicit equation of these surfaces:  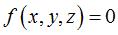with 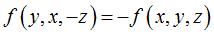; examples:

- the plane z = 0

- the hyperbolic paraboloid		video 1
- Plücker's conoid		video 2
- the symmetric parabolic Dupin cyclide		video 3
- the surface		video 4
- Costa's algebraic surface		video 5
- the surface		video 6

- the Enneper minimal surfaces, and Costa's minimal surface.

REMARK: all the surfaces of the above box have an equation of the type ; their isometry group is composed of the identity, the half-turn around Oz that does not swap the faces, the two half-turns around 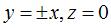, two reflections, and two rotorotations of order 4, this group is isomorphic to that of the isometries of the square.

See more generally the surfaces with rotational symmetry.
 
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017