Seifert surface

SEIFERT SURFACE

Surfaces studied by Seifert in 1934.
Herbert Seifert (1907-1996): German mathematician.
Sites :
Wikipedia
download seifertview software

A Seifert surface associated to a smooth closed curve without self-intersection of space (in other words, a representative of a knot) is an orientable connected compact surface without self-intersection the boundary of which is this curve.
The Seifert theorem provides the existence of this surface, that is of course not unique.

Much as the disk is obviously a Seifert surface associated to the trivial knot, one could think of obtaining a Seifert surface associated to the trefoil knot by joining each point of a curve to the farthest point of the curve by a segment line. However, the surface obtained in none other than the Moebius strip with 3 half-twists, which is not orientable.

To get a Seifert surface with a trefoil knot as boundary, we can trace a segment line between a pair of vertices at the top and make it move to a pair of vertices at the bottom, three times (figure at the center), and complete the two triangles. The resulting surface has indeed two faces (note for example that the upper face of the upper triangle leads to the upper face of the bottom triangle).

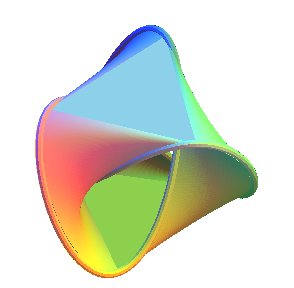After stylizing this, here is what we could get (on the left, a personal view, on the right, a view obtained by the software seifertview)

Opposite, the example of the Hopf link; the surface was obtained by moving a segment line joining the two disks (like in the previous examples, it is therefore a portion of ruled surface).

The notion of Seifert surface can be extended to links.
Opposite, the example of the Hopf link; the surface was obtained by moving a segment line joining the two disks (like in the previous examples, it is therefore a portion of ruled surface).

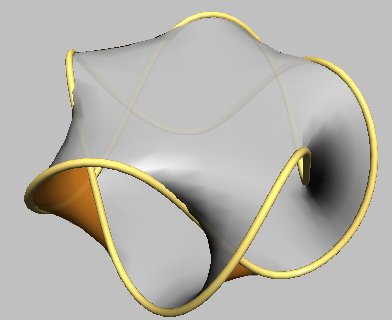
The trefoil knot and the Hopf link are toroidal links of type (p, 2 ) to which the same process as above can be applied to obtain a Seifert surface; below, the first four examples:

type of the link (2,2): Hopf link (3,2): trefoil knot (4,2): Salomon knot
prime link 4₁² (5,2)

Representation as a table with twisted legs made by Alain Esculier

Rounded representation (obtained by seifertview)

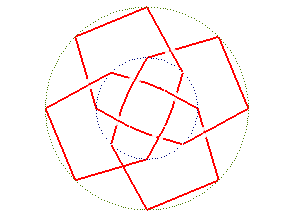
We can "add a tray" to the table above; by twisting the upper props in the opposite direction than the bottom props, we get 3 remarkable knots or links:

double table with 2 legs:
figure-eight knot double table with 3 legs:
Borromean rings double table with 4 legs:
prime knot 8₁₈

Representation as a table with twisted legs made by Alain Esculier

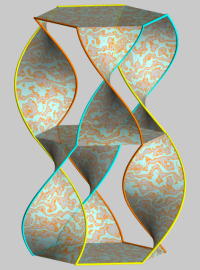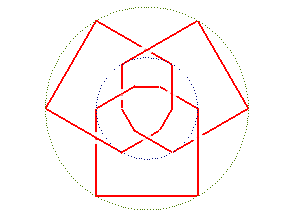
Conical projection of the knot

Rounded representation (seifertview)

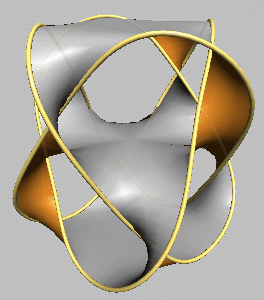More generally, a table with p trays and q legs, with the legs all twisted in the same direction, corresponds to the the toroidal link of type (p, q).
Any knot or link can be represented by this method, with any number of trays and legs, having any number of twists.

next surface previous surface 2D curves 3D curves surfaces fractals polyhedra

To get a Seifert surface with a trefoil knot as boundary, we can trace a segment line between a pair of vertices at the top and make it move to a pair of vertices at the bottom, three times (figure at the center), and complete the two triangles. The resulting surface has indeed two faces (note for example that the upper face of the upper triangle leads to the upper face of the bottom triangle).
After stylizing this, here is what we could get (on the left, a personal view, on the right, a view obtained by the software seifertview)

type of the link	(2,2): Hopf link	(3,2): trefoil knot	(4,2): Salomon knot prime link 4₁²	(5,2)
Representation as a table with twisted legs made by Alain Esculier
Rounded representation (obtained by seifertview)

	double table with 2 legs: figure-eight knot	double table with 3 legs: Borromean rings	double table with 4 legs: prime knot 8₁₈
Representation as a table with twisted legs made by Alain Esculier
Conical projection of the knot
Rounded representation (seifertview)