TORUS (GEOMETRIC NOTION)


| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
TORUS (GEOMETRIC NOTION)






| From the Latin torus "cushion, bulge".
Illustrative names: inner tube, life preserver, etc... |
| Cylindrical equation: Toroidal parametrization: Cartesian parametrization the coordinate lines of which are the meridian and parallel circles: Cartesian parametrization the coordinate lines of which are the Villarceau and parallel circles, in the case a > b ( Rational quartic surface. With the first parametrization: First fundamental quadratic form: Surface element: Second fundamental quadratic form: Gaussian curvature: Mean curvature: Volume and area for
|
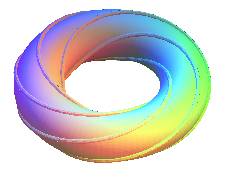
The torus is the surface generated by the revolution
of a circle (C) around a line (D) of its plane; it is therefore
a tube with constant diameter and circular
bore.
Here (D) is the axis Oz, b (minor
radius of the torus) the radius of (C) and a (major
radius of the torus) the distance from its center to (D).
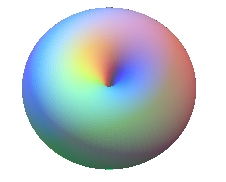
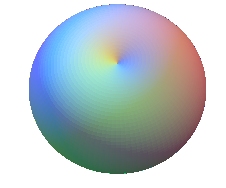
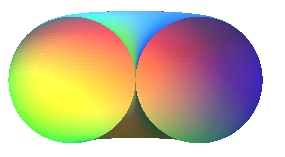
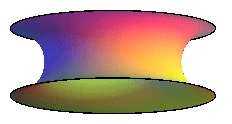
If (D) is secant to the circle (),
we get the spindle torus, shaped like a pumpkin or a cherry with
the limit cases of the sphere, if (D) is a diameter (a =
0), and the horn torus if (D) is a tangent of the circle
(a = b).
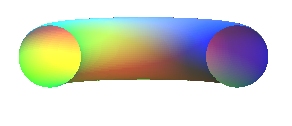
Otherwise (usual case a > b) we get a ring
torus, shaped like an inner tube.
The torus is a fourfold circled
surface: except the meridians (sections by the planes passing by the axis
of revolution) and the parallels (sections by the planes orthogonal to
the axis), there exist two families of circles obtained by the sections
by the bitangent planes of the torus, called Villarceau circles:
 |
 |
 |
 |
The curves traced on the torus are the spirics
(or toroidal curves).
See, in particular, the plane
sections, the geodesics,
the asymptotic lines
and the rhumb
lines of the torus.
For the contour of the projection of a torus, see toroid.
The inverse surfaces of the torus are the Dupin
cyclides.
For a special torus, see Wilmore
torus.
For the torus as a topological notion, see the next surface.
See also the Bohemian dome, Clifford's torus, and the sine tori.
A torus with its Villarceau circles, museum of the charity
of Notre-Dame, Strasbourg, 16th century.
See also this beautiful virtual
sculpture
  |
 |
 |
| Americans call the torus donut like the pastry, but in gastronomy, there are other tori like the onion rings... | Lots of fruits are shaped (very approximately) like the internal part of a spindle torus (above, the fruit of the cacao tree). For the external part, think of a tomato. | These fan vaults are shaped like the internal parts of the horn torus. |
A pulley is a half-torus |
 |
 |
| net surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL, Jacques MANDONNET 2017