A triple orthogonal system of surfaces consists in three given families with one parameter such that at any point common to three representatives of each family, the three tangent planes of the surfaces are 2 by 2 orthogonal. This notion generalizes to 3D the notion of double orthogonal systems of curves.
According to the Dupin theorem, two surfaces taken among two of the families of the system intersect along curvature lines.
 

If the three families are given in a parametric form: , fixed u, variable v,w for the first family, fixed v, variable u,w for the second one,  fixed w, variable u,v for the third one,  then the three families form a triple orthogonal system iff  (in other words, the columns of the Jacobian matrix of  are orthogonal to one another).

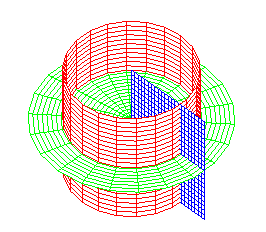
A first series of examples is provided by a given double orthogonal system  translated perpendicularly to its plane (the three orthogonal families are composed of two families of cylinders based on the initial curves and the family of planes orthogonal to the direction of translation); the triple orthogonal system is parametrized by .
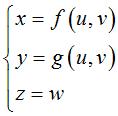
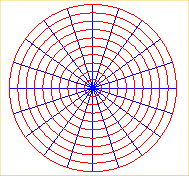
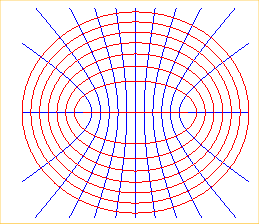
Some examples (first family, fixed u, in red, second one, fixed v, in blue, third one, fixed w, in green):
 
 

double orthogonal system	associated cylindrical triple system	parametrization	equations of the three families	name of the coordinate system (u,v,w)
	planes			Cartesian coordinates
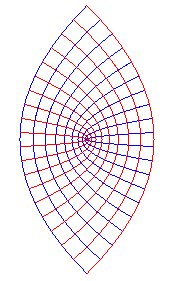
	cylinders of revolution, planes			cylindrical coordinates
	parabolic cylinders, planes			parabolic cylindrical coordinates
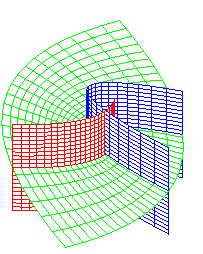
	elliptic cylinders, hyperbolic cylinders, planes			elliptic cylindrical coordinates

A second series is provided by a given double orthogonal system  rotated around an axis of its plane (or rather an axis of symmetry to avoid conical points); the orthogonal families are composed of two families of surfaces of revolution based on the initial curves and the family of planes passing by the axis of rotation; if the rotation is around Oz, then the triple orthogonal system is parametrized by .
Some examples:
 

double orthogonal system	associated triple system of revolution	parametrization	equations of the three families	name of the coordinate system (u,v,w)
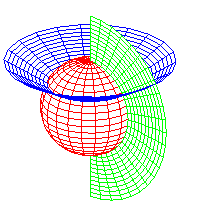
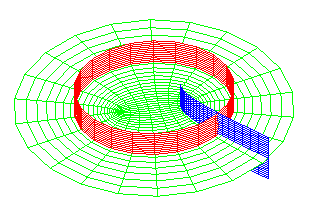
	spheres, cones, planes			spherical coordinates
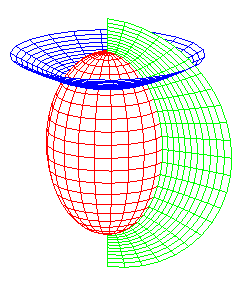
	prolate ellipsoids, two-sheeted hyperboloids, planes			prolate ellipsoidal coordinates
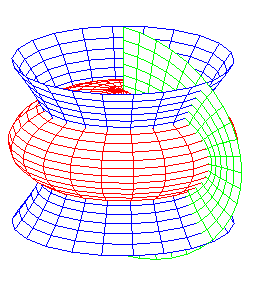
	oblate ellipsoids, one-sheeted hyperboloids, planes			oblate ellipsoidal coordinates
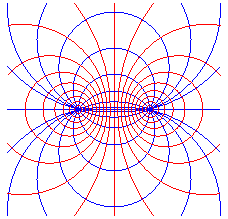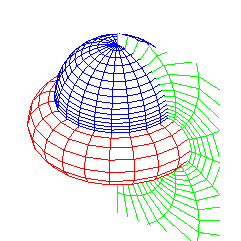
	ring tori, spheres, planes			toroidal coordinates
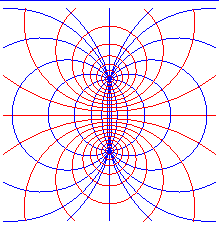	spheres, spindle tori, planes			bispherical coordinates

A third series is obtained by the images by an inversion of a triple orthogonal system, the resulting system still being a triple orthogonal system (since the map is conformal).
 

initial orthogonal system	2D equivalent	triple system	parametrization	equations of the three families	name of the coordinate system (u,v,w)
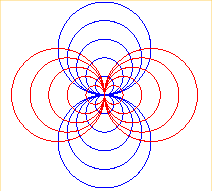orthogonal planes (associated to the Cartesian coordinates)		= three singular orthogonal beams of spheres			trispherical coordinates
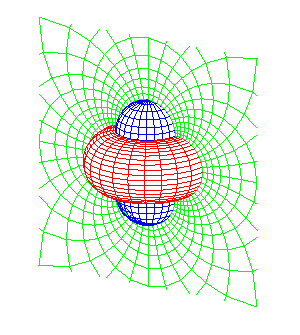
system associated to the cylindrical coordinates	the inverse triple orthogonal system of the cylindrical coordinates is none other than the double system composed of two beams of orthogonal circles rotated around Oz...	horn tori, planes, spheres			inverse cylindrical coordinates

The spherical coordinates are invariant under inversion.

Fourth series: systems of homofocal quadrics.
 

triple system	parametrization	intervals of definition	equations of the three families	name of the coordinate system (u,v,w)
ellipsoids, one-sheeted hyperboloids, two-sheeted hyperboloids		if :		homofocal ellipsoidal coordinates; see also quadric.
elliptic paraboloids turned upward, hyperbolic paraboloids, elliptic paraboloids turned downward		if :		homofocal paraboloidal coordinates; see also hyperbolic paraboloid
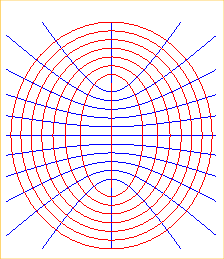
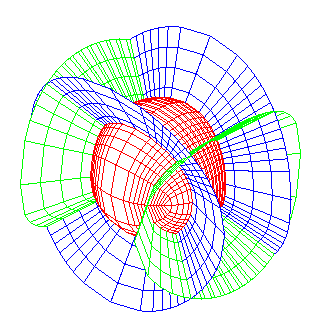spheres, elliptic cones. Notice the double orthogonal system of biquadratics on the sphere (remember that on the sphere, any line is a curvature line).		if :		conical coordinates

 
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017