Notion defined by Weingarten in 1861 then studied by Hopf in 1951. Julius Weingarten (1836-1910): German mathematician. Link: www.encyclopediaofmath.org/index.php/Weingarten_surface REF : [KÜHNEL] page 93

A surface is said to be a Weingarten surface if there exists a relation, that does not depend on the parameters, between the mean curvature and the total curvature (or between the principal curvatures).

Examples : obviously, the surfaces with constant mean or total curvature (of witch the developable surfaces), but also all toutes les surfaces of revolution : éliminate 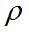between both expressions of the curvatures ; for example, the ellipsoid of revolution 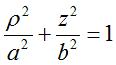 presents the relation  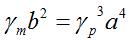between it's curvatures.
Theorem of Beltrami and Dini (1865) : the ruled surfaces that are of Weingarten are the developable surfaces and the ruled helicoids.
Theorem of Voss (1959) : the compact analytic surfaces of genus 0 that are of Weingarten are rotation surfaces; see for example the case where the curvatures are proportional.
 
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2019