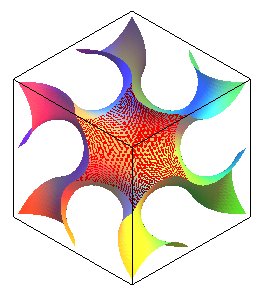
Les 2 figures ont été réalisées
à partir de l'équation
qui donne une surface non minimale proche du véritable gyroïde.
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
GYROÏDE
Gyroid,
Gyroide
| Surface étudiée et ainsi nommée
par A.
H. Schoen en 1970.
Alan Hugh Schoen (1924-...): mathématicien américain. Sites : wikipedia anglais page de Alan H. Schoen meet the gyroid www.susqu.edu/brakke/evolver/examples/periodic/gyroid/gyroid.html these de Scherer bugman123.com/MinimalSurfaces/index.html |
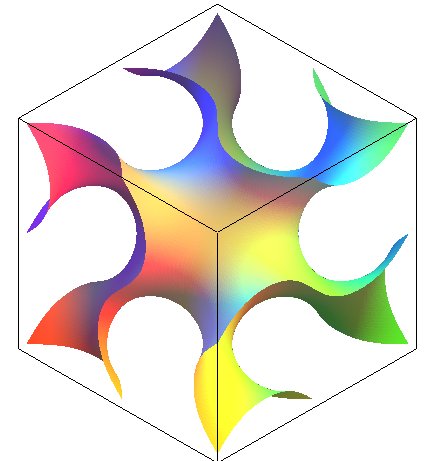
| Le gyroïde est une surface
minimale triplement périodique dont le pavé élémentaire,
est reproduit ci-contre.
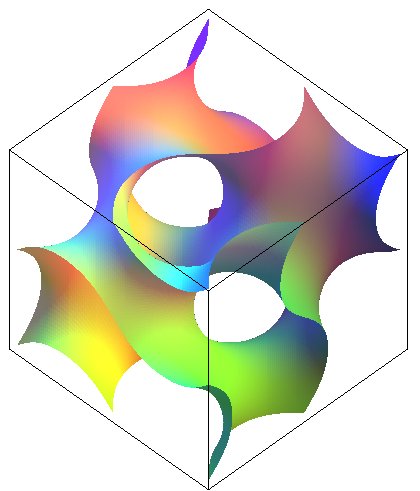
Les 2 figures ont été réalisées
à partir de l'équation |
 |
 |
| Le pavé élémentaire est formé de 8 hexagones gauches isométriques, dont 6 ont un sommet au centre du pavé. |
 |
 |
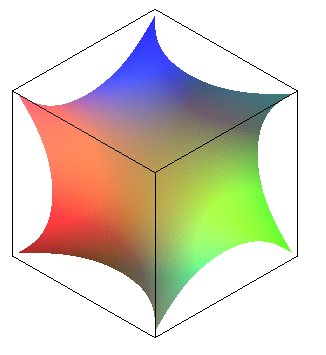
| Le gyroïde complet sépare l'espace en deux zones isométriques, comme pour la surface P de Schwarz. |  |
Comparer avec la surface
de Neovius.

Gyroïde intersecté par une sphère, par Alain Esculier |

Où ????? |

Similitudes avec le corail cerveau... |

ou avec une fleur de douche... |
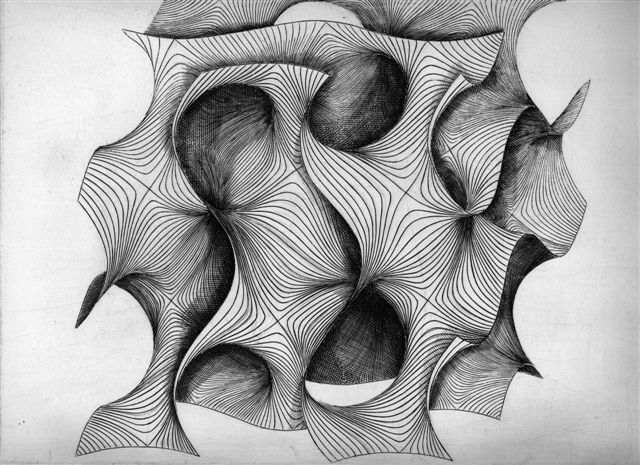

Gravures de gyroïdes avec lignes de courbures et lignes asymptotiques,
par Patrice Jeener, avec
son aimable autorisation.
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2014