Surface étudiée par Catalan en 1855. Eugène Charles Catalan (1814-1894) : mathématicien franco-belge. Autres appellations : surface réglée à plan directeur, cylindroïde.

 

Paramétrisation cartésienne : , réunion des droites Du passant par   et dirigées par  avec . Équation cartésienne réduite des surfaces de Catalan de plan directeur xOy ne comportant qu'une seule droite dans chaque plan parallèle à xOy :  (réunion des droites ), donnant un conoïde pour .

Une surface de Catalan est une surface réglée dont les génératrices restent parallèles à un plan fixe appelé plan directeur, autrement dit, une surface réglée dont le cône directeur est plan.

Exemples : les cylindres, les conoïdes, les hélicoïdes réglés à plan directeur.
 
 

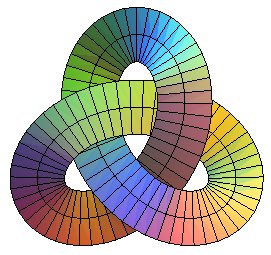
En reprenant les premières notations ci-dessus, un exemple intéressant est celui où  ; les génératrices sont alors orthogonales à la courbe décrite par M, et parallèles au plan orthogonal à . Ci-contre, le cas où cette courbe est un noeud de trèfle. Paramétrisation de cette surface : [cos(u)+2*cos(2*u), sin(u)-2*sin(2*u), 2*sin(3*u)]+v*[(8*cos(u)^2-cos(u)-4)/(-32*cos(u)^3+24*cos(u)+17)^(1/2), -sin(u)*(8*cos(u)+1)/(-32*cos(u)^3+24*cos(u)+17)^(1/2), 0].

La famille des droites s'appuyant sur deux courbes données et parallèles à un plan donné engendre une surface de Catalan. Prenant par exemple comme plan xOy, on obtient :
 

Paramétrisation cartésienne : , réunion des droites Du passant par  et .

Exemple d'une surface de Catalan s'appuyant sur deux sinusoïdes.

Ne pas confondre avec la surface minimale de Catalan.
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2020