CÔNE ELLIPTIQUE
Elliptical
cone, elliptischer Kegel

| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CÔNE ELLIPTIQUE
Elliptical
cone, elliptischer Kegel

| Autre nom : cône du second degré (en sous-entendant : non décomposé). |
| Équation réduite : Les sections par le plan z = k sont des ellipses de demi-axes ak/h et bk/h. Quadrique réglée développable. Paramétrisation cartésienne : Paramétrisation dont les lignes de coordonnées sont les lignes de courbure (cas Demi grand angle au sommet : demi petit angle au sommet : Volume du tronc de cône entre les plans z=0 et z=h : Autre équation réduite dans le cas où l'un des 2 angles au sommet est droit : |
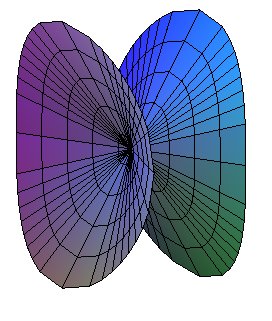 |
Un cône elliptique est un cône de directrice une ellipse ; il est défini à isométrie près par ses deux angles au sommet.
Caractérisation : cône du second degré
non décomposé en deux plans.
| Contrairement aux apparences, tout cône elliptique
contient des cercles.
Si l'on tourne le plan z = h d'un angle Ainsi, le cône elliptique est aussi un cône circulaire oblique. |
 |
Voir les lignes de niveau et de pente du cône
ici.
Comparer avec le cylindre
elliptique et voir aussi à cubique
circulaire focale.
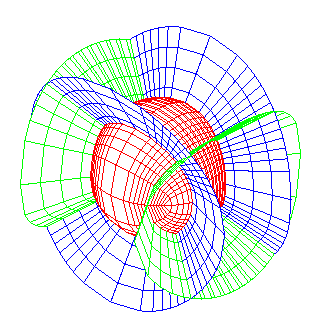
Système
triple orthogonal dont deux familles sont formées de cônes
elliptiques.
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2020