Coussin

COUSSIN DE BOULIGAND
Bouligand cushion, Bouligandsches Kissen

Surface étudiée par Bouligand en 1928 [bouligand, géométrie analytique, pb ENS 1928, p 487].
Nom maison.

Équation cartésienne du coussin seul :

.
Équation cartésienne de la surface complète, tournée d'un huitième de tour par rapport à la précédente :

ou encore

, le coussin seul étant obtenu pour

.
Paramétrisation du coussin seul :

.
Surface quartique.

© Alain Esculier	Le coussin de Bouligand est le lieu des points dont la somme des distances à deux droites fixes perpendiculaires est constant (les deux droites sont les diagonales du coussin). Remarque : ces coussins peuvent être vus comme les frontières des boules de la norme de : .
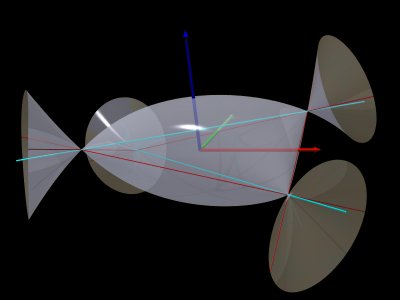	La surface complète est le lieu des points où la somme ou la différence de la distance aux droites est constante. Elle possède 4 points coniques, et 4 droites passant par eux. Les sections de cette surface par les plans x ou y = cte sont des ellipses ou des hyperboles, les sections par les plans , sont des réunions de paraboles, et les courbes de niveau z = cte sont des généralisations de cruciformes.
	Généralisation : lieu des points où la somme ou la différence de la distance à deux droites quelconques est constante. On obtient toujours une quartique à 4 points coniques.