Cubique réglée

(SURFACE) CUBIQUE RÉGLÉE
Ruled Cubic surface, kubische Regelfläche

Les cubiques réglées sont les surfaces réglées,algébriques de degré 3.

Voir sur cette page la démonstration des affirmations ci-dessous.

Excepté les cônes et cylindres de directrice une cubique plane, les autres cubiques réglées, dites "gauches" peuvent toutes être définies de la manière suivante :

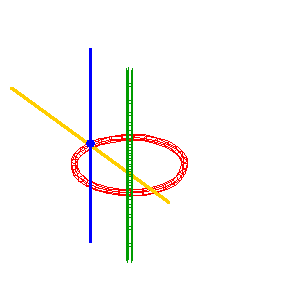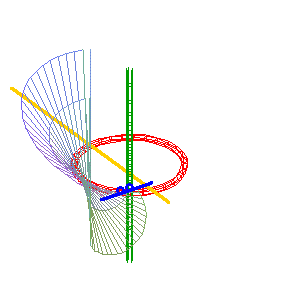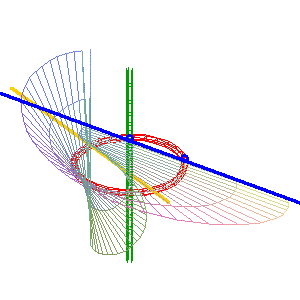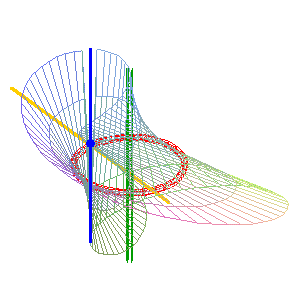
Etant donné une conique (C) située dans un plan (P), une droite (D₁), coupant (P) en O, une homographie entre les points A de (C) et B de (D₁) telle que O ne soit pas un point double, la cubique réglée est la réunion des droites (AB).

Figure montrant la construction d'une homographie entre la conique (C) et la droite (D₁), par l'intermédiaire d'une droite (d) du plan de la conique

Il y a alors deux classes d'équivalence projective complexes suivant que la droite (D₁) et la conique (C) sont sécantes en O (cas spécial des surfaces dites "surfaces réglées de Cayley", à ne pas confondre avec "la" surface de Cayley) ou non.

Dans le cas non sécant, la surface possède une autre directrice (D₂) rencontrant la conique (C) de sorte que la surface, ayant donc deux directrices rectilignes (D₁) et (D₂) est une surface conoïdale, et peut se définir comme la réunion des droites rencontrant (D₁), (D₂) et (C) ; la droite (D₂) est ligne double de la surface et contient deux points de pincement K et K' de la surface correspondant aux points où la génératrice forme avec la directrice (D₁) un plan tangent à la conique (C).
Ces deux points de pincement sont réels ou imaginaires suivant que l'on peut mener depuis O des tangentes réelles ou non à la conique (C), et ces deux cas forment deux classes d'équivalence projectives réelles distinctes.
Dans la première (points-pinces réels) se trouvent le conoïde de Plücker et le parapluie de Whitney, et dans la deuxième (points-pinces imaginaires) se trouvent le conoïde de Zindler et la surface de Möbius.

Remarque : lorsque O est point double de l'homographie ci-dessus, la surface définie dégénère en une quadrique.

Les cubiques réglées gauches sont toutes rationnelles, et sont des cas particulier de surfaces de Steiner.

Cas non spécial sans point pince réel
(b = 0) : la droite simple (D₁) (verte) est intérieure au cercle, l'autre droite est la droite double (D₂) .
Ici, la surface obtenue est la surface de Möbius.

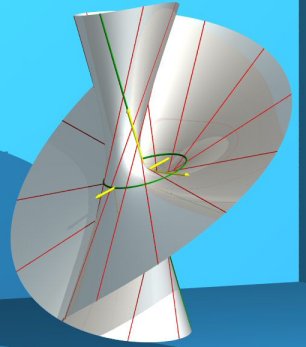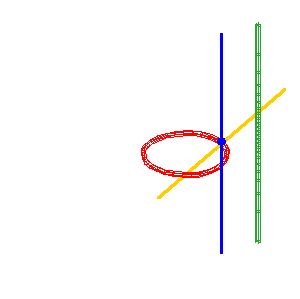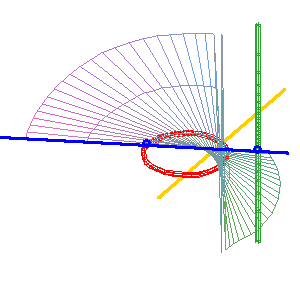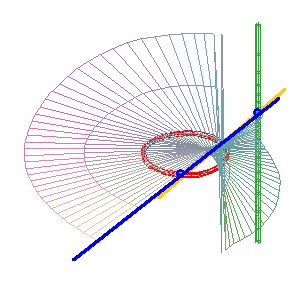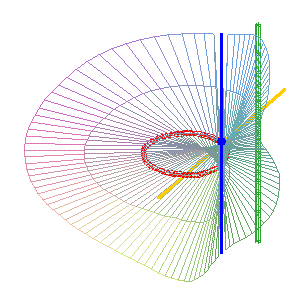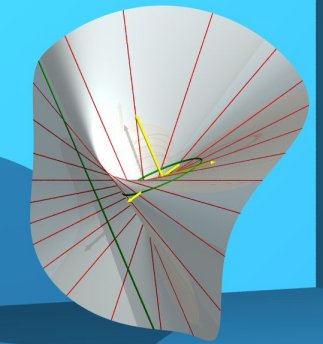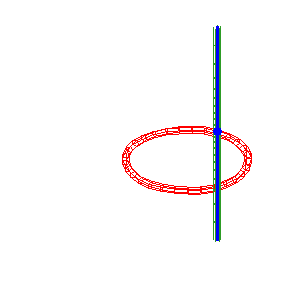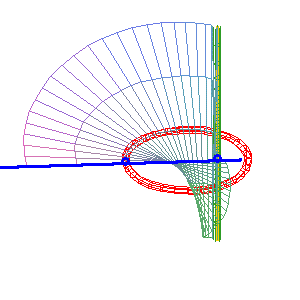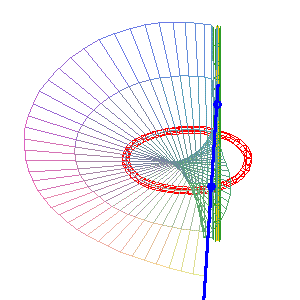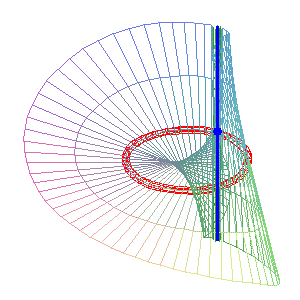
Cas non spécial avec deux points de pincement réels (b = -2a) : la droite simple (verte) est extérieure au cercle.

Cas spécial (b = –a) :
surface réglée de Cayley
la droite simple (D₁) (verte) est sécante au cercle et confondue avec (D₂) .

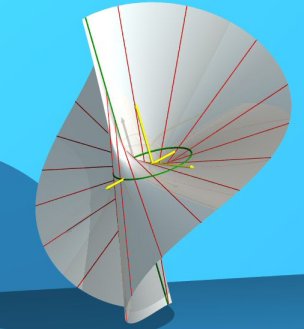Pour les animations ci-dessus, nous avons choisi
pour conique (C) le cercle , de point courant
et pour droite simple (D₁) la droite , de point courant (la transformation est bien homographique).
La droite double (D₂) est alors , de point courant .

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres