Surface développable

SURFACE DÉVELOPPABLE
Developable (or torsal, or flat) surface, Torse (oder abwickelbare Fläche)

Notion étudiée par Leonhard Euler en 1777 et Gaspard Monge en 1775/80.
Voir cet article d'Etienne Ghys et ce site suédois.

Équation aux dérivées partielles pour une surface explicite z = f (x, y) (notations de Monge) : rt = s² (exprimant que tous les points sont paraboliques).
Pour une surface implicite f(x,y,z)=0 : .
Pour une surface réglée (S) réunion des droites D_u:
1) Si les droites D_u sont définies par un point et un vecteur directeur , la paramétrisation cartésienne de (S) est: , et la CNS de développabilité est (la distance entre la droite D_u et la droite D_u+du vaut ).
Le point appartenant à l'arête de rebroussement est .
Cas particulier où la paramétrisation est : développable des tangentes à la courbe .
Première forme quadratique fondamentale : ???
2) M=M(u) décrivant une courbe gauche, a, b, c étant trois fonctions de u, la réunion des droites passant par M et dirigées par est une surface développable ssi .
3) Autre méthode (rotoïde de pas infini) : M=M(u) décrivant une courbe gauche, , , et étant les vecteur normal et binormal de cette courbe, et l'angle l'angle de torsion (voir les notations) :
Paramétrisation : où a et b sont des constantes.
Courbure de Gauss nulle.
Lignes de courbure : les génératrices et leurs trajectoires orthogonales.
Lignes asymptotiques : les génératrices.
Géodésiques : les courbes qui se développent en des droites (donc en particulier les génératrices).

Une surface développable est une surface réglée que l’on peut faire rouler sans glisser sur un plan, le contact se faisant le long d’une droite, comme pour un cylindre ou un cône. Concrètement, c'est une surface que l'on obtient en déformant sans pliure une feuille de papier cartonné.

Les définitions suivantes caractérisent les surfaces développables :

DEF 1 : une surface développable est une surface réglée dont toute génératrice est stationnaire, c'est-à-dire telle que le plan tangent à la surface est le même en tout point de la génératrice.
Conditions directement équivalentes :
    - 1.1 surface réglée dont les génératrices sont paraboliques.
    - 1.2 surface réglée telle que la normale principale le long d'une génératrice engendre un plan ;
    - 1.3 surface réglée dont les génératrices sont des lignes de courbure (voir à normalie).
    - 1.4 surface réglée telle que les plans parallèles aux plans tangents passant par un point donné enveloppent le cône directeur de la surface (réunion des droites parallèles aux génératrices passant par le point).

DEF 2 : Une surface développable est une surface où chaque génératrice est sécante avec les génératrices infiniment voisines (cf. ci-dessus D_u et D_u+du sont sécantes), éventuellement à l'infini (cas des cylindres).

DEF 3 : une surface développable est une surface réglée dont les génératrices possèdent une enveloppe (éventuellement réduite à un point (cas des cônes), voire un point à l'infini (cas des cylindres)).

DEF 4 : une surface développable est une surface de Monge à génératrice rectiligne (surface engendrée par le mouvement d’une droite fixe d'un plan mobile dont tous les points ont un vecteur vitesse orthogonal à ce plan).

DEF 5 : une surface développable est une surface enveloppe d'une famille de plans à un paramètre.

En particulier toute famille de plans passant par un point décrivant une courbe gauche enveloppe une surface développable ; cas particuliers :
- les plans sont les plans osculateurs à la courbe (contenant la tangente et la normale) : la développable engendrée est la réunion des tangentes à la courbe et la courbe est l’arête de rebroussement de la surface.

- les plans sont les plans rectifiants de la courbe (contenant la tangente et la binormale) : la courbe gauche est alors une géodésique de la surface et la surface est appelée la développable rectifiante (en anglais : rectifying torse) de cette courbe ; la génératrice passant par M (la droite rectifiante) est dirigée par le vecteur de rotation instantané du repère de Frenet ; le point de l'arête de rebroussement est .
- les plans sont les plans normaux à la courbe : la développable engendrée est la surface polaire de la courbe gauche ; la courbe gauche est alors une développante de la surface.

Ce sont des surfaces dont tous les points sont paraboliques (ou torsaux, i.e. à courbure totale nulle ou encore tels que l'un des rayons de courbure principaux est infini) ; ce qui est remarquable, c'est que réciproquement, toute surface sans méplat dont tous les points sont paraboliques est incluse dans une surface développable.

Les surfaces développables sont des surfaces applicables sur le plan, et réciproquement, toute surface applicable sur le plan de classe C²est incluse dans une surface développable. Lorsqu'on applique la surface sur le plan, on dit qu'on la développe.
La condition de classe C²est importante car on peut construire des surfaces applicables sur un plan de classe C¹non réglées ; on raconte que lorsque Darboux énonça, dans un cours à l'école normale supérieure à la fin du 19ème que "toute surface développable est réglée", l'élève Henri Lebesgue sortit son mouchoir et dit : "Montrez-moi les génératrices ! " (cf Berger p. 148).

Lorsque l'on fait rouler une surface développable sur un plan, la trace d'une courbe tracée sur la surface donne une courbe plane dont la courbure est la courbure géodésique de la courbe sur la surface. En particulier, les géodésiques et les cercles géodésiques se développent en des droites et cercles du plan.
La trace de l'arête de rebroussement (dont la courbure égale la courbure géodésique) est une courbe ayant même relation entre l'abscisse curviligne et la courbure (mais sans torsion) et les tangentes s'appliquent l'une sur l'autre ; inversement, ceci permet de voir une surface développable comme le résultat de la torsion d'une courbe plane munie de ses tangentes.

Exemples :
    - les cônes
    - les cylindres,
    - l’hélicoïde développable (dont l'arête de rebroussement est une hélice circulaire, résultant de la torsion d'un cercle), et
    - plus généralement, les surfaces d'égale pente (dont les génératrices ont un angle constant avec un plan fixe).
    - la développable des tangentes à la parabole gauche.
    - le ruban de Möbius développable
    - l'oloïde
    - les surfaces développables obtenues par pliage

Il existe en général une unique surface développable contenant deux courbes données : l'enveloppe des plans tangents communs aux deux courbes.
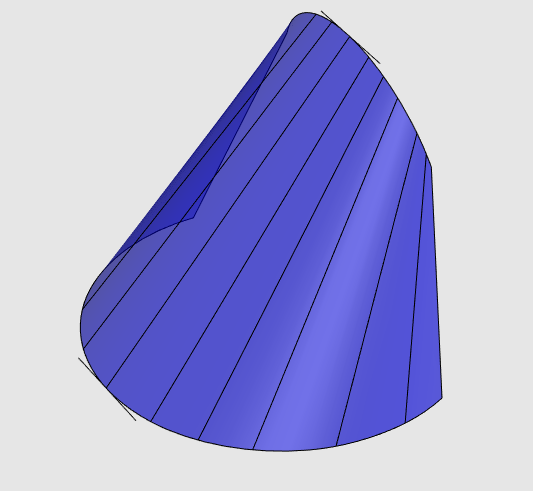
La condition d'existence est que toute tangente à la première courbe soit sécante à une tangente à la deuxième courbe, et réciproquement (donc pas de surface développable s'appuyant sur deux droites non coplanaires par exemple).
Cette condition est par exemple réalisée si les deux courbes sont situées dans deux plan sécants (et que leurs tangentes ont toutes les directions possibles dans ces plans).
Ci-contre, figure dûe à Robert March, montrant la construction dans le cas de deux cercles (voir aussi l'oloïde).
On remarquera que le contour apparent de la surface est rectiligne, propriété caractéristique des surfaces développables.

Si les deux courbes sont parallèles, la surface développable est la réunion des droites perpendiculaires aux deux courbes. Par exemple, si l'on prolonge les traverses de ces voies ferrées de montagnes russes, on obtient deux surfaces développables.

Plusieurs oeuvres du sculpteur Antoine Pevsner représentent des surfaces développables, comme cette maquette de la "colonne développable de la victoire" .

Voir aussi à normalie.

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres